题目内容
 如图所示,气缸放置在水平平台上,活塞质量为10kg,横截面积50cm2,厚度1cm,气缸全长21cm,气缸质量20kg,大气压强为1×105 Pa,当温度为7℃时,活塞封闭的气柱长10cm,若将气缸倒过来放置时,活塞下方的空气能通过平台上的缺口与大气相通.g取10m/s2,封闭的气体可视为理想气体,在转动过程中没有发生漏气.求:
如图所示,气缸放置在水平平台上,活塞质量为10kg,横截面积50cm2,厚度1cm,气缸全长21cm,气缸质量20kg,大气压强为1×105 Pa,当温度为7℃时,活塞封闭的气柱长10cm,若将气缸倒过来放置时,活塞下方的空气能通过平台上的缺口与大气相通.g取10m/s2,封闭的气体可视为理想气体,在转动过程中没有发生漏气.求:①若气柱温度不变,气柱达到新的平衡时的长度;
②缓慢升高气柱的温度,当活塞刚好接触平台时气柱的温度.
分析:①气体发生等温变化,由玻意耳定律可以求出空气柱的长度.
②由盖吕萨克定律可以求出气体的温度.
②由盖吕萨克定律可以求出气体的温度.
解答:解:(1)对于封闭气体:
初态:P1=P0+
=1×105+
=1.2×105Pa,
气缸倒置后气体压强:P2=P0-
=1×105-
=0.8×105Pa,
气体发生等温变化,由玻意耳定律得:
P1L1S=P2L2S,
解得:L2=
L1=
×10cm=15cm;
(2)气体温度:T2=T1=280K,体积:V2=L2S=15S,
活塞刚好接触平台时气体体积 V3=L3S=(21-1)S=20S,
由盖吕萨克定律得:
=
,即
=
,则T3≈373K.
所以t3=T3-273°C=373°C-273°C=100℃
答:①若气柱温度不变,气柱达到新的平衡时的长度为15cm.②缓慢升高气柱的温度,当活塞刚好接触平台时气柱的温度为1000C.
初态:P1=P0+
| mg |
| s |
| 10×10 |
| 50×10-4 |
气缸倒置后气体压强:P2=P0-
| mg |
| S |
| 10×10 |
| 50×10-4 |
气体发生等温变化,由玻意耳定律得:
P1L1S=P2L2S,
解得:L2=
| P1 |
| P2 |
| 1.2×105 |
| 0.8×105 |
(2)气体温度:T2=T1=280K,体积:V2=L2S=15S,
活塞刚好接触平台时气体体积 V3=L3S=(21-1)S=20S,
由盖吕萨克定律得:
| V2 |
| T2 |
| V3 |
| T3 |
| 15S |
| 280 |
| 20S |
| T3 |
所以t3=T3-273°C=373°C-273°C=100℃
答:①若气柱温度不变,气柱达到新的平衡时的长度为15cm.②缓慢升高气柱的温度,当活塞刚好接触平台时气柱的温度为1000C.
点评:应用玻意耳定律与盖吕萨克定律即可正确解题,本题的解题关键是求出各状态的气体压强.

练习册系列答案
相关题目
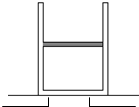 如图所示,气缸放置在水平平台上,活塞质量为10kg,横截面积50cm2,厚度1cm,气缸全长21cm,气缸质量20kg,大气压强为1×105Pa,当温度为7℃时,活塞封闭的气柱长10cm,若将气缸倒过来放置时,活塞下方的空气能通过平台上的缺口与大气相通.g取10m/s2求:
如图所示,气缸放置在水平平台上,活塞质量为10kg,横截面积50cm2,厚度1cm,气缸全长21cm,气缸质量20kg,大气压强为1×105Pa,当温度为7℃时,活塞封闭的气柱长10cm,若将气缸倒过来放置时,活塞下方的空气能通过平台上的缺口与大气相通.g取10m/s2求: 如图所示,气缸放置在水平地面上,缸内封闭一定质量的气体,活塞横截面积为S,外界大气压强为P0,气缸内电热丝热功率为P,测得通电时间t内活塞缓慢向左移动距离为h,气缸向外界放出热量为Q,不计活塞与气缸之间的摩擦,则在时间t内缸内气体内能的变化量为( )
如图所示,气缸放置在水平地面上,缸内封闭一定质量的气体,活塞横截面积为S,外界大气压强为P0,气缸内电热丝热功率为P,测得通电时间t内活塞缓慢向左移动距离为h,气缸向外界放出热量为Q,不计活塞与气缸之间的摩擦,则在时间t内缸内气体内能的变化量为( ) (2008?虹口区二模)如图所示,气缸放置在水平平台上,活塞质量为10kg,横截面积50cm2,厚度1cm,气缸全长21cm,气缸质量20kg,大气压强为1×105Pa,当温度为7℃时,活塞封闭的气柱长10cm.若将气缸缓慢倒过来放置时,活塞下方的空气能通过平台上的缺口与大气相通.g取10m/s2.求:
(2008?虹口区二模)如图所示,气缸放置在水平平台上,活塞质量为10kg,横截面积50cm2,厚度1cm,气缸全长21cm,气缸质量20kg,大气压强为1×105Pa,当温度为7℃时,活塞封闭的气柱长10cm.若将气缸缓慢倒过来放置时,活塞下方的空气能通过平台上的缺口与大气相通.g取10m/s2.求: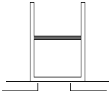 如图所示,气缸放置在水平平台上,活塞质量为10kg,横截面积50cm2,厚度1cm,气缸全长21cm,大气压强为1×105Pa,当温 度为7℃时,活塞封闭的气柱长10cm,若将气缸倒过来放置时,活塞下方的空气 能通过平台上的缺口与大气相通.g取10m/s2,不计活塞与气缸之间的摩擦,保留三位有效数字.
如图所示,气缸放置在水平平台上,活塞质量为10kg,横截面积50cm2,厚度1cm,气缸全长21cm,大气压强为1×105Pa,当温 度为7℃时,活塞封闭的气柱长10cm,若将气缸倒过来放置时,活塞下方的空气 能通过平台上的缺口与大气相通.g取10m/s2,不计活塞与气缸之间的摩擦,保留三位有效数字.