题目内容
总质量为M的列车，沿水平直线轨道匀速前进，其末节车厢质量为m，中途脱节，司机发觉时，机车已行驶了L的距离.于是立即关闭油门，除去牵引力，设运动的阻力与重力成正比，机车的牵引力是恒定的，求列车完全停下时，列车两部分间的距离是多少？
解析：列车在脱钩前做匀速运动，其牵引力F=kmg脱钩后，尾部车厢在阻力作用下匀减速运动，前部机车在关闭油门加前速运动，在关闭油门后做减速运动，依据题意，可以作出如图所示运动的示意图.
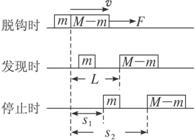
从运动过程来看，前部车厢和尾部车厢均做阶段性匀变速运动，可用牛顿第二定律和运动学公式联立求解，但运算相当烦琐，可考虑用动能定理求解，而且可以不分段处理，整体考虑.
以机车为研究对象，受力情况为：脱钩发现前受牵引力和阻力，发现后只受阻力，对其脱钩前后的全过程，根据动能定理有：
FL-k(M-m)gs2=0-
(M-m)v02①
以末节车厢为研究对象，脱钩后只受阻力作用，根据动能定理有：
-kmgs1=0-
mv02②
又F=kmg③
联立①②③可解得：Δs=s2-s1=
L.
练习册系列答案
相关题目
