题目内容
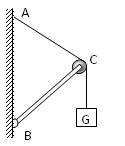
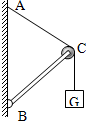
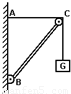
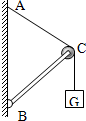如图所示，杆BC的B端铰接在竖直墙上，另一端C为一滑轮．重物G上系一绳经过滑轮固定于墙上A点处，杆恰好平衡．若将绳的A端沿墙向下移，再使之平衡（BC杆、滑轮、绳的质量及摩擦均不计），则（ ）分析：由于杆一直平衡，故绳子对杆的压力一定沿着杆的方向，而同一根绳子的张力处处相等，根据平行四边形定则分析即可．
解答：解：由于杆一直平衡，对两根细线的拉力的合力一定在杆的方向上；
又由于而同一根绳子的张力处处相等，故两根细线的拉力一定相等且等于物体的重力G；
根据平行四边形定则，合力一定在角平分线上，由于两拉力的夹角不断减小，故两个拉力的合力不断变大，故杆受到的压力不断变大；
故选C．
又由于而同一根绳子的张力处处相等，故两根细线的拉力一定相等且等于物体的重力G；
根据平行四边形定则，合力一定在角平分线上，由于两拉力的夹角不断减小，故两个拉力的合力不断变大，故杆受到的压力不断变大；
故选C．
点评：本题关键是要明确连个细线的拉力的合力沿着杆子的方向，且两个细线的拉力等于物体的重力，然后根据平行四边形定则进行分析判断．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
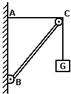如图所示，杆BC的B端用铰链接于竖直墙上，另一端C为一定滑轮．重物G系一绳经过滑轮固定于墙上的A点，杆恰好平衡．若将绳的A端沿墙向上移，再使之平衡，杆重、滑轮大小及各处摩擦均可省略，则（ ）
