题目内容
（14分）一滑块经水平轨道AB，进入竖直平面内的四分之一圆弧轨道BC，已知滑块的质量m=0．6kg，在
A点的速度vA=8m/s，AB长x=5m， 滑块与水平轨道间的动摩擦因数μ=0．15，圆弧轨道的半径R=2m，滑块离开C点后竖直上升h=0．2m，
取g=10m/s2。求：
（1）滑块滑到B点前的加速度和滑块恰好滑过B点时的加速度。
（2）滑块在圆弧轨道BC段克服摩擦力所做的功。
A点的速度vA=8m/s，AB长x=5m， 滑块与水平轨道间的动摩擦因数μ=0．15，圆弧轨道的半径R=2m，滑块离开C点后竖直上升h=0．2m，取g=10m/s2。求：
（1）滑块滑到B点前的加速度和滑块恰好滑过B点时的加速度。
（2）滑块在圆弧轨道BC段克服摩擦力所做的功。
（1）
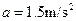，方向水平向右；
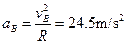，方向竖直向上
（2）
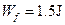
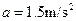，方向水平向右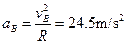；，方向竖直向上（2）
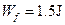
（1）滑块滑到B点前的加速度大小：
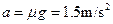(2分） 方向水平向右(1分）
滑块由A到B得过程，利用动能定理得：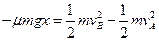
(3分）
解得：
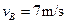(1分）
滑块滑到B点时的加速度大小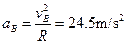： (2分）
方向竖直向上 (1分）
（2）滑块在圆弧轨道BC段克服摩擦力所做的功，利用动能定理得：
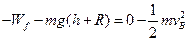(2分）
所以
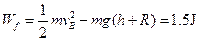(2分）
说明：利用其它方法，正确的同样给分
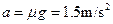(2分） 方向水平向右(1分）滑块由A到B得过程，利用动能定理得：
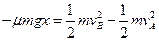(3分）解得：
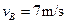(1分）滑块滑到B点时的加速度大小：
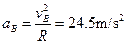(2分）方向竖直向上 (1分）
（2）滑块在圆弧轨道BC段克服摩擦力所做的功，利用动能定理得：
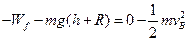(2分）所以
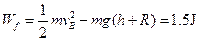(2分）说明：利用其它方法，正确的同样给分
练习册系列答案
相关题目
圆弧形光滑轨道ABC，放置在竖直平面内，轨道半径为R，在A点与水平地面AD相接，地面与圆心O等高，MN是放在水平地面上长为3R、厚度不计的垫子，左端M正好位于A点．将一个质量为m的小球从A处正上方某处由静止释放，不考虑空气阻力，若小球能从C点射出并打到垫子上，小球距离A点的高度在什么范围．
，则小物块从A运动到B的过程中，下列说法正确的是 （ ）