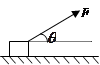题目内容
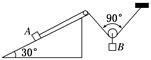
(14分)跨过定滑轮的轻绳两端,分别系着物体A和物体B,物体A放在倾角为θ的斜面上(所示),已知物体A的质量为m,物体A与斜面的动摩擦因数为μ(μ<tanθ),滑轮的摩擦不计,要使物体A静止在斜面上,求物体B的质量的取值范围。(视最大静摩擦力等于滑动摩擦力)


m(sinθ-μcosθ)≤mB≤m(sinθ+μcosθ)
试题分析:先选物体B为研究对象,它受到重力mBg和拉力T的作用,根据平衡条件有:
T=mBg ① (2分)
再选物体A为研究对象,它受到重力mg、斜面支持力N、轻绳拉力T和斜面的摩擦力作用,假设物体A处于将要上滑的临界状态,则物体A受的静摩擦力最大,且方向沿斜面向下,这时A的受力情况如图所示,
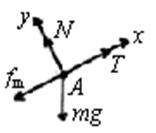
根据平衡条件有:
N-mgcosθ=0 ② (2分)
Tmax-fm- mgsinθ=0 ③ (2分)
由摩擦力公式知:fm=μN ④ (1分)
以上四式联立解得mB=m(sinθ+μcosθ) (2分)
再假设物体A处于将要下滑的临界状态,则物体A受的静摩擦力最大,且方向沿斜面向上,根据平衡条件有:
Tmin+fm- mgsinθ=0 ⑤ (2分)
①②④⑤四式联立解得mB="m(sinθ-μcosθ)" (2分)
综上所述,物体B的质量的取值范围是:
m(sinθ-μcosθ)≤mB≤m(sinθ+μcosθ) (1分)

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

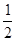
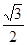

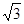


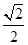 m B.
m B.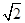 m
m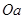 与竖直方向的夹角为
与竖直方向的夹角为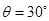 ,则F的最小值
,则F的最小值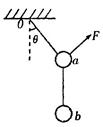
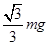
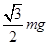
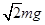
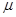 (设最大静摩擦力等于滑动摩擦力),对物体施加一个与水平方向成
(设最大静摩擦力等于滑动摩擦力),对物体施加一个与水平方向成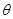 角的力F,求物体在水平面上运动时力F的值应满足的条件。(重力加速度为g)
角的力F,求物体在水平面上运动时力F的值应满足的条件。(重力加速度为g)