题目内容
 如图所示的传送带,其水平部分ab的长度为2m,倾斜部分bc的长度为4m,bc与水平面的夹角为α=37°.将一小物块A(可视为质点)轻轻放于a端的传送带上,物块A与传送带间的动摩擦因数为μ=0.25.传送带沿图示方向以v=2m/s的速度匀速运动,若物块A始终未脱离皮带.(g=10m/s2,sin37°=0.6,cos37°=0.8)
如图所示的传送带,其水平部分ab的长度为2m,倾斜部分bc的长度为4m,bc与水平面的夹角为α=37°.将一小物块A(可视为质点)轻轻放于a端的传送带上,物块A与传送带间的动摩擦因数为μ=0.25.传送带沿图示方向以v=2m/s的速度匀速运动,若物块A始终未脱离皮带.(g=10m/s2,sin37°=0.6,cos37°=0.8)求:(1)小物块从a端被传送到b端所用的时间.
(2)小物块被传送到c端时的速度大小.
(3)若当小物块到达b 端时,传送带的速度突然增大为v′,问v′的大小满足什么条件可以使小物块在倾斜传送带bc上运动所用的时间最短?
分析:(1)根据牛顿第二定律求出小物块的加速度,并求出当物块的速度达到2m/s时的位移,判断出物体的运动情况,从而求出小物块从a端被传送到b端所用的时间.
(2)根据摩擦力与下滑力的关系,判断出物体的运动情况,根据牛顿第二定律求出加速度,再根据运动学公式求出小物块被传送到c端时的速度大小.
(3)当物体一直有向下的摩擦力,则加速度最大,做匀加速直线运动,运动的时间最短.所以物体的速度在整个过程中小于传送带的速度.
(2)根据摩擦力与下滑力的关系,判断出物体的运动情况,根据牛顿第二定律求出加速度,再根据运动学公式求出小物块被传送到c端时的速度大小.
(3)当物体一直有向下的摩擦力,则加速度最大,做匀加速直线运动,运动的时间最短.所以物体的速度在整个过程中小于传送带的速度.
解答: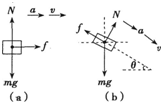 解:(1)小物块在水平传送带上运动时受力如图a所示,加速度a1=μg=2.5m/s2
解:(1)小物块在水平传送带上运动时受力如图a所示,加速度a1=μg=2.5m/s2
加速过程的位移为x1=
=0.8m,则A在水平带上先加速后匀速
t=
+
=1.4s
故小物块从a端被传送到b端所用的时间为1.4s.
(2)小物块在倾斜传送带上运动时受力如图b所示,
因为mgsin37°>μmgcos37°,则A在bc段做匀加速运动,
加速度a2=g(sin37°-μcos37°)=4m/s2
由运动学公式 vc2-v2=2albc
解得:vc=6m/s
故小物块被传送到c端时的速度大小为6m/s.
(3)要使小物块在倾斜传送带上运动时所用时间最短,则加速度要最大,即传送带对小物块的滑动摩擦力沿带向下a3=g(sin37°+μcos37°)=8m/s2,且一直加速.
由v′2-v2=2a3lbc
解得v3=2
m/s
则v的大小应满足v≥2
m/s可以使小物块在倾斜传送带bc上运动的时间最短.
 解:(1)小物块在水平传送带上运动时受力如图a所示,加速度a1=μg=2.5m/s2
解:(1)小物块在水平传送带上运动时受力如图a所示,加速度a1=μg=2.5m/s2加速过程的位移为x1=
| v2 |
| 2a1 |
t=
| v |
| a1 |
| lab-x1 |
| v |
故小物块从a端被传送到b端所用的时间为1.4s.
(2)小物块在倾斜传送带上运动时受力如图b所示,
因为mgsin37°>μmgcos37°,则A在bc段做匀加速运动,
加速度a2=g(sin37°-μcos37°)=4m/s2
由运动学公式 vc2-v2=2albc
解得:vc=6m/s
故小物块被传送到c端时的速度大小为6m/s.
(3)要使小物块在倾斜传送带上运动时所用时间最短,则加速度要最大,即传送带对小物块的滑动摩擦力沿带向下a3=g(sin37°+μcos37°)=8m/s2,且一直加速.
由v′2-v2=2a3lbc
解得v3=2
| 17 |
则v的大小应满足v≥2
| 17 |
点评:本题是动力学问题,关键根据加速度方向与速度方向的关系,理清物体的运动情况,运用牛顿第二定律和运动学公式求解.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 如图所示的传送带,其水平部分ab的长度为2m,倾斜部分bc的长度为4m,bc与水平面的夹角为α=37°,将一小物块A(可视为质点)轻轻放于a端的传送带上,物块A与传送带间的动摩擦因数为μ=0.25,当传送带沿图示方向以v=2m/s的速度匀速运动时,若物块A经过b端时未脱离传送带且没有速率损失,试求:
如图所示的传送带,其水平部分ab的长度为2m,倾斜部分bc的长度为4m,bc与水平面的夹角为α=37°,将一小物块A(可视为质点)轻轻放于a端的传送带上,物块A与传送带间的动摩擦因数为μ=0.25,当传送带沿图示方向以v=2m/s的速度匀速运动时,若物块A经过b端时未脱离传送带且没有速率损失,试求:
 如图所示的传送带,其水平部分AB长SAB=3.2m,BC部分与水平面夹角θ为37°,长度SBC=22m,一小物体P与传送带的动摩擦因数?=0.25,皮带沿A至B方向运行,速率恒为v=12m/s,若把物体P无初速度的放在A点处,它将被传送带送到C点(B处为一小曲面,不改变速度的大小,只改变速度的方向),且物体P不脱离传送带.求
如图所示的传送带,其水平部分AB长SAB=3.2m,BC部分与水平面夹角θ为37°,长度SBC=22m,一小物体P与传送带的动摩擦因数?=0.25,皮带沿A至B方向运行,速率恒为v=12m/s,若把物体P无初速度的放在A点处,它将被传送带送到C点(B处为一小曲面,不改变速度的大小,只改变速度的方向),且物体P不脱离传送带.求 sin37°=0.6, cos37°=0.8)
sin37°=0.6, cos37°=0.8)