题目内容
如图所示，匀强电场场强的方向与水平方向成θ=30°角，有一带电量为q，质量为m的小球，用长为L的绝缘细线悬挂于O点，当静止时，细线恰被拉成水平方向，求：（1）小球的电性及匀强电场场强E的大小；
（2）若改变匀强电场方向，使其竖直向下，求小球摆到最低点时的速度及绳子的拉力大小．
分析：（1）对小球受力分析，根据小球所受电场力的方向与场强方向间的关系判断小球的电性，由平衡条件求出场强的大小．
（2）由动能定理可以求出小球摆到最低点时的速度，由牛顿第二定律可以求出绳子的拉力．
（2）由动能定理可以求出小球摆到最低点时的速度，由牛顿第二定律可以求出绳子的拉力．
解答：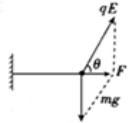
解：（1）小球受力如图所示，小球所受电场力的方向与场强方向相同，小球带正电；
由平衡条件得：qEsin30°=mg，解得：E=
；
（2）小球下摆过程中，由动能定理得：
mgL+qEL=
mv2-0，
小球做圆周运动，在最低点，由牛顿第二定律得：
T-mg-qE=m
，
解得：v=
，T=9mg；
答：（1）小球带正电，匀强电场场强E的大小为
；
（2）小球摆到最低点时的速度为
，绳子的拉力大小为9mg．
解：（1）小球受力如图所示，小球所受电场力的方向与场强方向相同，小球带正电；由平衡条件得：qEsin30°=mg，解得：E=
| 2mg |
| q |
（2）小球下摆过程中，由动能定理得：
mgL+qEL=
| 1 |
| 2 |
小球做圆周运动，在最低点，由牛顿第二定律得：
T-mg-qE=m
| v2 |
| L |
解得：v=
| 6gL |
答：（1）小球带正电，匀强电场场强E的大小为
| 2mg |
| q |
（2）小球摆到最低点时的速度为
| 6gL |
点评：正电荷所受电场力方向与场强方向相同，负电荷所受电场力方向与场强方向相反；对球正确受力分析，应用平衡条件、动能定理即可正确解题．
练习册系列答案
名校课堂系列答案
相关题目
（2012?金山区一模）如图所示，M，N是水平放置的一对正对平行金属板，其中M板中央有一小孔O，板间存在竖直向上的匀强电场，AB是一根长为9L的轻质绝缘细杆，在杆上等间距地固定着10个完全相同的带电小球（小球直径略小于孔），每个小球带电荷量为q，质量为m，相邻小球间的距离为L，小球可视为质点，不考虑带电小球之间库仑力．现将最下端的小球置于O处，然后将AB由静止释放，AB在运动过程中始终保持竖直，经观察发现，在第二个小球进入电场到第三个小球进入电场前这一过程中，AB做匀速直线运动．已知MN两板间距大于细杆长度．试求：