题目内容
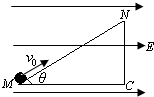 如图所示,长为L,倾角为θ的光滑绝缘斜面处于水平向右的匀强电场中.一电荷量为+q,质量为m的小球,以初速度v0由斜面底端的M点沿斜面上滑,到达斜面顶端N的速度仍为v0,则( )
如图所示,长为L,倾角为θ的光滑绝缘斜面处于水平向右的匀强电场中.一电荷量为+q,质量为m的小球,以初速度v0由斜面底端的M点沿斜面上滑,到达斜面顶端N的速度仍为v0,则( )分析:带电小球从底端运动到顶端,重力做负功,电场力做正功,而支持力不做功.而两处速度相等,则重力做的功与电场力做功之和为零.所以可以确定小球在何处的电势能高.同时由倾角可确定重力与电场力的关系.
解答:解:A、小球以初速度v0由斜面底端的M点沿斜面上滑,到达斜面顶端N的速度仍为v0,根据动能定理,重力做功与电场力做功相等,有:qEx=mgh,所以E=
=
.故A正确,B错误.
C、M、N两点间的电势差U=ELcosθ=
.故C错误.
D、从M到N电场力做正功,电势能减小,N点的电势能小于M点的电势能.故D错误.
故选A.
| mgh |
| qx |
| mgtanθ |
| q |
C、M、N两点间的电势差U=ELcosθ=
| mgLsinθ |
| q |
D、从M到N电场力做正功,电势能减小,N点的电势能小于M点的电势能.故D错误.
故选A.
点评:由带电小球受到分析得:重力、支持力与电场力,且三力均不变.若存在加速度,则带小球也不可能到达N点的速度仍不变的,所以三力处于平衡状态.故带电小球做的是匀速直线运动.

练习册系列答案
相关题目