题目内容
质量均为m的两个梯形木块，紧挨着放在水平面上，梯形木块一角为θ，如图，现用水平力推它们一起向右运动，不计一切摩擦，为不使两木块之间发生相对滑动，推力F的大小的取值范围是0＜F≤2mgtanθ
0＜F≤2mgtanθ
．分析：对整体根据牛顿第二定律列式得到整体的加速度，再隔离对右边的物体受力分析，由牛顿第二定律可得F最大值．
解答：解：推力为0时木块之间一定不滑动；
对整体根据牛顿第二定律列式得：
F=2ma
故整体加速度为：
a=
①
对右侧的物块进行分析：
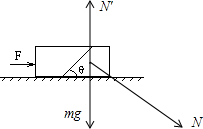
由牛顿第二定律可知，木块B的加速度：
a=
所以AB之间刚好不会发生相对滑动时，
推力F=2ma=2m×
=2Nsinθ
再对左侧物体受力分析：
若两者不相对滑动，则有：
mg=N″cosθ
又：N=N″
得：
N=
代入：F=2Nsinθ
得F最大值为：
F=2
sinθ=2mgtanθ
故答案为：0＜F≤2mgtanθ
对整体根据牛顿第二定律列式得：
F=2ma
故整体加速度为：
a=
| F |
| 2m |
对右侧的物块进行分析：
由牛顿第二定律可知，木块B的加速度：
a=
| Nsinθ |
| m |
所以AB之间刚好不会发生相对滑动时，
推力F=2ma=2m×
| Nsinθ |
| m |
再对左侧物体受力分析：
若两者不相对滑动，则有：
mg=N″cosθ
又：N=N″
得：
N=
| mg |
| cosθ |
代入：F=2Nsinθ
得F最大值为：
F=2
| mg |
| cosθ |
故答案为：0＜F≤2mgtanθ
点评：本题主要是用好整体法和隔离法，这是在处理叠加体，连接体等情形常用的方法．
练习册系列答案
相关题目
