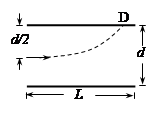题目内容
如图,在第一象限存在匀强磁场,磁感应强度方向垂直于纸面(xy平面)向外;在第四象限存在匀强电场,方向沿x轴负向。在y轴正半轴上某点以与x轴正向平行、大小为v0的速度发射出一带正电荷的粒子,该粒子在(d,0)点沿垂直于x轴的方向进人电场。不计重力。若该粒子离开电场时速度方向与y轴负方向的夹角为θ,求:
(1)电场强度大小与磁感应强度大小的比值;
(2)该粒子在电场中运动的时间。
(1)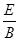 =
= ;(2)t=
;(2)t=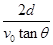
解析试题分析:(1)设磁感应强度的大小为B,粒子质量与所带电荷量分别为m和q,粒子进入磁场后做匀速圆周运动,并设其圆周运动的半径为r,根据牛顿第二定律和向心力公式有:qv0B=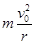 ①
①
由题设条件和图中几何关系可知:r=d ②
设电场强度大小为E,粒子进入电场后沿x轴负方向运动的速度大小为vx,由牛顿第二定律有:qE=max ③
根据运动学公式有:vx=axt,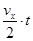 =d ④
=d ④
由于粒子在电场中做类平抛运动(如图),有:tanθ=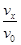 ⑤
⑤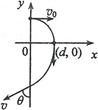
由①②③④⑤式联立解得: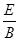 =
=
(2)由④⑤式联立解得:t=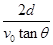
考点:本题主要考查了带电粒子在交替复合场中的运动问题,属于中档题。

练习册系列答案
相关题目


 cm的圆形区域内,有一个方向垂直纸面向外的水平匀强磁场,磁感应强度大小为B=0.10T。竖直平行放置的两金属板A、K相距为d,连接在电路中,电源电动势E=91V,内阻r=1.0Ω,定值电阻R1=10Ω,滑动变阻器R2的最大阻值为80Ω,S1、S2为A、K板上的两个小孔,且S1、S2跟O在竖直极板的同一直线上,OS2=2R,另有一水平放置的足够长的荧光屏D,O点跟荧光屏D点之间的距离为H。比荷为2.0×105C/kg的离子流由S1进入电场后,通过S2向磁场中心射去,通过磁场后落到荧光屏D上。离子进入电场的初速度、重力、离子之间的作用力均可忽略不计。问:
cm的圆形区域内,有一个方向垂直纸面向外的水平匀强磁场,磁感应强度大小为B=0.10T。竖直平行放置的两金属板A、K相距为d,连接在电路中,电源电动势E=91V,内阻r=1.0Ω,定值电阻R1=10Ω,滑动变阻器R2的最大阻值为80Ω,S1、S2为A、K板上的两个小孔,且S1、S2跟O在竖直极板的同一直线上,OS2=2R,另有一水平放置的足够长的荧光屏D,O点跟荧光屏D点之间的距离为H。比荷为2.0×105C/kg的离子流由S1进入电场后,通过S2向磁场中心射去,通过磁场后落到荧光屏D上。离子进入电场的初速度、重力、离子之间的作用力均可忽略不计。问:
 cm的圆形区域内,有一个方向垂直纸面向外的水平匀强磁场,磁感应强度大小为B=0.10T。竖直平行放置的两金属板A、K相距为d,连接在电路中,电源电动势E=91V,内阻r=1.0Ω,定值电阻R1=10Ω,滑动变阻器R2的最大阻值为80Ω,S1、S2为A、K板上的两个小孔,且S1、S2跟O在竖直极板的同一直线上,OS2=2R,另有一水平放置的足够长的荧光屏D,O点跟荧光屏D点之间的距离为H。比荷为2.0×105C/kg的离子流由S1进入电场后,通过S2向磁场中心射去,通过磁场后落到荧光屏D上。离子进入电场的初速度、重力、离子之间的作用力均可忽略不计。问:
cm的圆形区域内,有一个方向垂直纸面向外的水平匀强磁场,磁感应强度大小为B=0.10T。竖直平行放置的两金属板A、K相距为d,连接在电路中,电源电动势E=91V,内阻r=1.0Ω,定值电阻R1=10Ω,滑动变阻器R2的最大阻值为80Ω,S1、S2为A、K板上的两个小孔,且S1、S2跟O在竖直极板的同一直线上,OS2=2R,另有一水平放置的足够长的荧光屏D,O点跟荧光屏D点之间的距离为H。比荷为2.0×105C/kg的离子流由S1进入电场后,通过S2向磁场中心射去,通过磁场后落到荧光屏D上。离子进入电场的初速度、重力、离子之间的作用力均可忽略不计。问:

 ,极板长为L,极板间有一匀强电场,U为两极板间的电压,电子从极板左端的正中央以初速
,极板长为L,极板间有一匀强电场,U为两极板间的电压,电子从极板左端的正中央以初速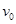 射入,其方向平行于极板,并打在极板上的D点,如图所示。电子的电荷量用e表示,质量用
射入,其方向平行于极板,并打在极板上的D点,如图所示。电子的电荷量用e表示,质量用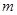 表示,重力不计。求
表示,重力不计。求