题目内容
 如图所示,一个圆柱形容器的底部半径与高均为b,当容器未装液体时,从某点A恰能看到底部边缘的B点.当容器装满某种液体时,仍沿AB方向看去,恰好能看到底部中心O,已知光在真空中的传播速度为c,试求光在此液体中的传播速度.
如图所示,一个圆柱形容器的底部半径与高均为b,当容器未装液体时,从某点A恰能看到底部边缘的B点.当容器装满某种液体时,仍沿AB方向看去,恰好能看到底部中心O,已知光在真空中的传播速度为c,试求光在此液体中的传播速度.分析:作出装满液体后的光路图,根据折射定律求出折射率的大小,结合v=
求出光在液体中的传播速度.
| c |
| n |
解答: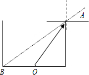 解:设O点射出的光线与竖直方向上的夹角为θ,射出后折射角为α.根据几何关系得,sinθ=
解:设O点射出的光线与竖直方向上的夹角为θ,射出后折射角为α.根据几何关系得,sinθ=
=
.
sinα=
=
则折射率n=
=
则光在液体中的速度v=
=
.
答:光在此液体中的传播速度为
c.
 解:设O点射出的光线与竖直方向上的夹角为θ,射出后折射角为α.根据几何关系得,sinθ=
解:设O点射出的光线与竖直方向上的夹角为θ,射出后折射角为α.根据几何关系得,sinθ=| b | ||
|
| ||
| 2 |
sinα=
| 2b | ||
|
2
| ||
| 5 |
则折射率n=
| sinα |
| sinθ |
2
| ||
| 5 |
则光在液体中的速度v=
| c |
| n |
| ||
| 4 |
答:光在此液体中的传播速度为
| ||
| 4 |
点评:解决本题的关键掌握折射定律以及光在介质中的速度与折射率的关系.

练习册系列答案
相关题目
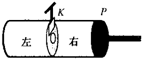 如图所示,一个圆柱形气缸,中间有一隔板,板壁上有一孔,并有一闸门K,右侧有一不漏气的活塞P,开始时闸门K关闭,气缸左侧充有一些空气,活塞P位于气缸右侧,隔板与活塞P间为真空,气缸和隔板都是导热的,第一步:打开闸门K,空气将充满气缸的左右两侧;第二步:向左缓慢推动活塞P,直至紧挨隔板,关闭闸门K,然后再把活塞P拉至气缸右侧的初始位置.下面的说法中正确的是( )
如图所示,一个圆柱形气缸,中间有一隔板,板壁上有一孔,并有一闸门K,右侧有一不漏气的活塞P,开始时闸门K关闭,气缸左侧充有一些空气,活塞P位于气缸右侧,隔板与活塞P间为真空,气缸和隔板都是导热的,第一步:打开闸门K,空气将充满气缸的左右两侧;第二步:向左缓慢推动活塞P,直至紧挨隔板,关闭闸门K,然后再把活塞P拉至气缸右侧的初始位置.下面的说法中正确的是( )| A、经过这样两步操作,气缸、活塞及缸内气体组成的系统又恢复到开始的状态,并且没有引起其他变化 | B、第一步操作后,气体充满左右两侧的过程中,气体要从外部吸收热量 | C、第二步操作过程中,气体要从外部吸收热量 | D、这整个过程中,有机械能向内能转化 |
 如图所示,一个圆柱形气缸,中间有一隔板,板壁上有一孔,并有一闸门K,右侧有一不漏气的活塞P,开始时闸门K关闭,气缸左侧充有一些空气,活塞P位于气缸右侧,隔板与活塞P间为真空,气缸和隔板都是导热的,第一步:打开闸门K,空气将充满气缸的左右两侧;第二步:向左缓慢推动活塞P,直至紧挨隔板,关闭闸门K,然后再把活塞P拉至气缸右侧的初始位置.下面的说法中正确的是( )
如图所示,一个圆柱形气缸,中间有一隔板,板壁上有一孔,并有一闸门K,右侧有一不漏气的活塞P,开始时闸门K关闭,气缸左侧充有一些空气,活塞P位于气缸右侧,隔板与活塞P间为真空,气缸和隔板都是导热的,第一步:打开闸门K,空气将充满气缸的左右两侧;第二步:向左缓慢推动活塞P,直至紧挨隔板,关闭闸门K,然后再把活塞P拉至气缸右侧的初始位置.下面的说法中正确的是( ) 如图所示,一个圆柱形气缸,中间有一隔板,板壁上有一孔,并有一闸门K,右侧有一不漏气的活塞P.开始时闸门K关闭,气缸左侧充有一些空气,活塞P位于气缸右侧,隔板与活塞P间为真空.气缸和隔板都是导热的.第一步:打开闸门K,空气将充满气缸的左右两侧;第二步:向左缓慢推动活塞P,直至紧挨隔板,关闭闸门K,然后再把活塞P拉至气缸右侧的初始位置.下面的说法中正确的是
如图所示,一个圆柱形气缸,中间有一隔板,板壁上有一孔,并有一闸门K,右侧有一不漏气的活塞P.开始时闸门K关闭,气缸左侧充有一些空气,活塞P位于气缸右侧,隔板与活塞P间为真空.气缸和隔板都是导热的.第一步:打开闸门K,空气将充满气缸的左右两侧;第二步:向左缓慢推动活塞P,直至紧挨隔板,关闭闸门K,然后再把活塞P拉至气缸右侧的初始位置.下面的说法中正确的是