题目内容
【题目】如图所示内壁光滑的环形槽半径为R,固定在竖直平面内,环形槽上的P、Q两点与环形槽圆心等高,质量均为m的小球(可视为质点)A和B,以等大的速率v0同时从P处向上、向下滑入环形槽,若在运动过程中两球均未脱离环形槽,设当地重力加速度为g,则下列叙述正确的是( )
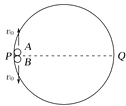
A. 两球第一次相遇时速度相同
B. 两球第一次相遇点在Q点
C. 小球A通过最高点时的机械能小于小球B通过最低点时的机械能
D. 小球A通过最高点和小球B通过最低点时对环形槽的压力差为6mg
【答案】D
【解析】由于两球在初始位置的机械能相等,故两球在环形槽内的任何位置的机械能都相等,故C错误;对小球A,由机械能守恒定律可得:![]() ,在最高点,由牛顿第二定律可得
,在最高点,由牛顿第二定律可得![]() ;对小球B,由机械能守恒定律可得:
;对小球B,由机械能守恒定律可得:![]() ,在最低点,由牛顿第二定律可得:
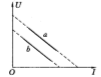
,在最低点,由牛顿第二定律可得:![]() ,联立可得:ΔF=FB-FA=6mg,故D正确;分别对两球受力分析,可知两球的重力在圆环切线方向的分力改变速度的大小,又因为两球从P点到Q点的路程相等,分别作出此过程的速率—时间图象,
,联立可得:ΔF=FB-FA=6mg,故D正确;分别对两球受力分析,可知两球的重力在圆环切线方向的分力改变速度的大小,又因为两球从P点到Q点的路程相等,分别作出此过程的速率—时间图象,
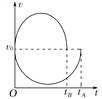
由图象可知小球B先到达Q点,故B错误;其相遇点在Q点的上方,由机械能守恒定律可知,两球第一次相遇时速度的大小相等,但方向不同,故A错误。所以D正确,ABC错误。

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目