题目内容
如图所示,两木块A、B由轻质弹簧连接,起初静止在光滑水平面上,某时刻一粒子弹以水平速度v击中木块A并留在其中,子弹打入木块的过程持续时间极短,可不考虑此过程中木块A的移动.已知木块A的质量为(M-m),木块B的质量为M,子弹的质量为m,弹簧原长为l,劲度系数为k,弹簧的弹性势能与形变量的对应关系式是Ep=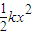 .如果此后过程中弹簧始终处于弹性限度内,且木块A、B不会发生直接碰撞.试求:
.如果此后过程中弹簧始终处于弹性限度内,且木块A、B不会发生直接碰撞.试求:(1)当弹簧压缩到最短时,木块B的速度大小.
(2)运动中弹簧出现的最大长度.

【答案】分析:(1)当弹簧压缩到最短时,A、B的速度相等.对于子弹、A、B木块组成的系统,合外力为零,动量守恒,由动量守恒定律列式求木块B的速度.
(2)子弹打入木块后,弹簧先被压缩,A减速,B加速,速度相等后,弹簧压缩到最短;接下来,A继续减速,B继续加速,B的速度大于A的速度,弹簧从压缩逐渐到伸长,伸长时,A加速,B减速,只要B的速度大于A的速度,弹簧继续伸长,当两者速度再次相等时,弹簧伸长到最长.可这样求解:子弹打入木块A的过程中,子弹和木块A系统动量守恒,求它们的共同速度,再根据系统的动量守恒、机械能守恒和速度相等的条件列式求弹簧最大的长度.
解答:解:(1)当弹簧压缩到最短时,A、B的速度相同,设为v,依动量守恒定律有:
mv=2Mv
解得:v=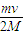
(2)子弹打入木块A的过程中,子弹和木块A系统动量守恒,设它们最后共同速度为v1,
mv=Mv1
解得:v1=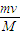
当弹簧达到最大长度时,两木块A、B速度相同仍为:
v=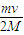
从子弹射入木块A后到两者具有共同速度弹簧最长过程中,由系统的机械能守恒得:
 kx
kx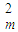 =
=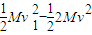
解得:xm=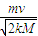
弹簧出现的最大长度为:
l=l+xm=l+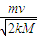
答:
(1)当弹簧压缩到最短时,木块B的速度大小为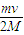 .
.
(2)运动中弹簧出现的最大长度为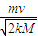 .
.
点评:本题是含有非弹性碰撞的过程,分析过程,挖掘出弹簧长度最大的条件是关键,再根据动量守恒和能量守恒结合求解.
(2)子弹打入木块后,弹簧先被压缩,A减速,B加速,速度相等后,弹簧压缩到最短;接下来,A继续减速,B继续加速,B的速度大于A的速度,弹簧从压缩逐渐到伸长,伸长时,A加速,B减速,只要B的速度大于A的速度,弹簧继续伸长,当两者速度再次相等时,弹簧伸长到最长.可这样求解:子弹打入木块A的过程中,子弹和木块A系统动量守恒,求它们的共同速度,再根据系统的动量守恒、机械能守恒和速度相等的条件列式求弹簧最大的长度.
解答:解:(1)当弹簧压缩到最短时,A、B的速度相同,设为v,依动量守恒定律有:
mv=2Mv
解得:v=
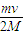
(2)子弹打入木块A的过程中,子弹和木块A系统动量守恒,设它们最后共同速度为v1,
mv=Mv1
解得:v1=
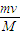
当弹簧达到最大长度时,两木块A、B速度相同仍为:
v=
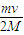
从子弹射入木块A后到两者具有共同速度弹簧最长过程中,由系统的机械能守恒得:
 kx
kx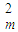 =
=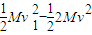
解得:xm=
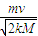
弹簧出现的最大长度为:
l=l+xm=l+
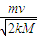
答:
(1)当弹簧压缩到最短时,木块B的速度大小为
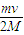 .
.(2)运动中弹簧出现的最大长度为
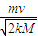 .
.点评:本题是含有非弹性碰撞的过程,分析过程,挖掘出弹簧长度最大的条件是关键,再根据动量守恒和能量守恒结合求解.

练习册系列答案
相关题目
 如图所示,两木块A、B用轻质弹簧连在一起,置于光滑的水平面上.一颗子弹水平射入木块A,并留在其中.在子弹打中木块A及弹簧被压缩的整个过程中,对子弹、两木块和弹簧组成的系统,下列说法中正确的是( )
如图所示,两木块A、B用轻质弹簧连在一起,置于光滑的水平面上.一颗子弹水平射入木块A,并留在其中.在子弹打中木块A及弹簧被压缩的整个过程中,对子弹、两木块和弹簧组成的系统,下列说法中正确的是( )| A、动量守恒、机械能守恒 | B、动量守恒、机械能不守恒 | C、动量不守恒、机械能守恒 | D、动量、机械能都不守恒 |
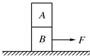
 如图所示,两木块A和B叠放在光滑水平面上,质量分别为m和M,A与B之间的最大静摩擦力为f,B与劲度系数为k的轻质弹簧连接构成弹簧振子.为使A和B在振动过程中不发生相对滑动,则它们的振幅不能大于
如图所示,两木块A和B叠放在光滑水平面上,质量分别为m和M,A与B之间的最大静摩擦力为f,B与劲度系数为k的轻质弹簧连接构成弹簧振子.为使A和B在振动过程中不发生相对滑动,则它们的振幅不能大于 如图所示,两木块A、B叠放在水平桌面上,现以水平拉力F拉B没有拉动,则以下说法正确的是( )
如图所示,两木块A、B叠放在水平桌面上,现以水平拉力F拉B没有拉动,则以下说法正确的是( ) 如图所示,两木块A、B由轻质弹簧连接,起初静止在光滑水平面上,某时刻一粒子弹以水平速度v0击中木块A并留在其中,子弹打入木块的过程持续时间极短,可不考虑此过程中木块A的移动.已知木块A的质量为(M-m),木块B的质量为M,子弹的质量为m,弹簧原长为l0,劲度系数为k,弹簧的弹性势能与形变量的对应关系式是Ep=
如图所示,两木块A、B由轻质弹簧连接,起初静止在光滑水平面上,某时刻一粒子弹以水平速度v0击中木块A并留在其中,子弹打入木块的过程持续时间极短,可不考虑此过程中木块A的移动.已知木块A的质量为(M-m),木块B的质量为M,子弹的质量为m,弹簧原长为l0,劲度系数为k,弹簧的弹性势能与形变量的对应关系式是Ep=