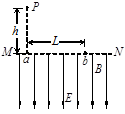题目内容
 如图所示,一带电的小球从P点自由下落,(不计空气阻力)P点距场区边界MN高为h,边界MN下方有方向竖直向下、电场场强为E的匀强电场,同时还有垂直于纸面的匀强磁场,小球从边界上的a 点进入重力场、电场与磁场的复合场后,恰能作匀速圆周运动,并从边界上的b点第一次穿出,已知ab=L,重力加速度为g.
如图所示,一带电的小球从P点自由下落,(不计空气阻力)P点距场区边界MN高为h,边界MN下方有方向竖直向下、电场场强为E的匀强电场,同时还有垂直于纸面的匀强磁场,小球从边界上的a 点进入重力场、电场与磁场的复合场后,恰能作匀速圆周运动,并从边界上的b点第一次穿出,已知ab=L,重力加速度为g.求:(1)小球进入复合场时速度大小
(2)该匀强磁场的磁感强度B的大小;
(3)小球从P 经a 至b 时,共需时间为多少?
分析:(1)粒子在磁场中做匀速圆周运动,则重力与电场力平衡,则由平衡关系可求得比荷;
(2)由几何关系可得粒子做圆周运动的半径,由牛顿第二定律可求得磁感应强度的大小;
(3)粒子由P到a做自由落体运动,由自由落体规律可求得下落时间;由a到b粒子做圆周运动,由转过的角度可求得转动的时间.
(2)由几何关系可得粒子做圆周运动的半径,由牛顿第二定律可求得磁感应强度的大小;
(3)粒子由P到a做自由落体运动,由自由落体规律可求得下落时间;由a到b粒子做圆周运动,由转过的角度可求得转动的时间.
解答:解:(1)由机械能守恒可知:
mgh=
mv2
得:v=
(2)粒子在复合场中做匀速圆周运动,则重力和电场力平衡,洛仑兹力提供做圆周运动的向心力,重力和电场力平衡,电场力方向向上,电场方向向下,
则为负电荷mg=Eq,比荷
=
粒子由a到b运动半周,由其受力方向根据左手定则可知磁场方向为垂直纸面向外
由牛顿第二定律可知:qvB=m
而由几何关系可知:L=2R
联立可得:B=2E
(3)由p到a时,h=
gt12
复合场中,粒子恰转过了180°,则转动时间:t2=
=
=
运动总时间:t=
+
答:(1)小球进入复合场时速度大小为
;
(2)该匀强磁场的磁感强度B的大小为2E
;
(3)小球从P 经a 至b 时,共需时间为
+
.
mgh=
| 1 |
| 2 |
得:v=
| 2gh |
(2)粒子在复合场中做匀速圆周运动,则重力和电场力平衡,洛仑兹力提供做圆周运动的向心力,重力和电场力平衡,电场力方向向上,电场方向向下,
则为负电荷mg=Eq,比荷
| q |
| m |
| g |
| E |
粒子由a到b运动半周,由其受力方向根据左手定则可知磁场方向为垂直纸面向外
由牛顿第二定律可知:qvB=m
| v2 |
| R |
而由几何关系可知:L=2R
联立可得:B=2E
| 2gh |
| 1 |
| gL |
(3)由p到a时,h=
| 1 |
| 2 |
复合场中,粒子恰转过了180°,则转动时间:t2=
| 1 |
| 2 |
| 2πm |
| qB |
| πm |
| qB |
| πL | ||
2
|
运动总时间:t=
|
| πL | ||
2
|
答:(1)小球进入复合场时速度大小为
| 2gh |
(2)该匀强磁场的磁感强度B的大小为2E
| 2gh |
| 1 |
| gL |
(3)小球从P 经a 至b 时,共需时间为
|
| πL | ||
2
|
点评:粒子在复合场的运动要注意几种特殊的运动,如粒子做匀速直线运动,则受力平衡;粒子做圆周运动,则重力一定与电场力平衡,洛仑兹力充当向心力.

练习册系列答案
相关题目
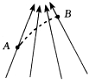 如图所示,一带电粒子只受电场力从A飞到B,径迹如图中虚线所示,下列说法正确的是( )
如图所示,一带电粒子只受电场力从A飞到B,径迹如图中虚线所示,下列说法正确的是( )| A、粒子带正电 | B、粒子加速度不断变小 | C、粒子在A点时动能较大 | D、B点场强小于A点场强 |
 如图所示,一带电为+q质量为m的小物块处于一倾角为37°的光滑斜面上,当整个装置处于一水平方向的匀强电场中时,小物块恰处于静止.若从某时刻起,电场强度减小为原来的1/2,求:(已知sin37°=0.6,cos37°=0.8)
如图所示,一带电为+q质量为m的小物块处于一倾角为37°的光滑斜面上,当整个装置处于一水平方向的匀强电场中时,小物块恰处于静止.若从某时刻起,电场强度减小为原来的1/2,求:(已知sin37°=0.6,cos37°=0.8)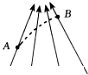 如图所示,一带电粒子只受电场力从A飞到B,径迹如图中虚线所示,下列说法正确的是( )
如图所示,一带电粒子只受电场力从A飞到B,径迹如图中虚线所示,下列说法正确的是( )