题目内容
如图所示,一质量为m的小球,用长为l的轻绳悬挂于O点,初始时刻小球静止于P点,第一次小球在水平拉力F作用下,从P点缓慢地移动到Q点,此时轻绳与竖直方向夹角为θ,张力大小为T1,第二次在水平恒力F′作用下,从P点开始运动并恰好能到达Q点,至Q点时轻绳中的张力大小为T2,关于这两个过程,下列说法中正确的是(不计空气阻力,重力加速度为g)( )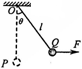
| A.第一个过程中,拉力F在逐渐变大,且最大值一定大于F′ |
| B.两个过程中,轻绳的张力均变大 |
C.T1=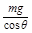 ,T2=mg ,T2=mg |
| D.第二个过程中,重力和水平恒力F′的合力的功率先增大后减小 |
AC
解析试题分析:第一次小球缓慢移动,因此,小球处于平衡状态,解得F=mgtanα,绳中张力T=mg/cosα,随着α的逐渐增大,力F、T逐渐增大,当α=θ时,有:Fm=mgtanθ,T1=mg/cosθ,在第二次运动过程中,根据动能定理有:-mgl(1-cosθ)+F′lsinθ=0,解得:F′=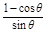 mg=
mg= ,故选项A正确;此过程中,小球恰能到达Q点,说明vQ=0,根据牛顿第二定律可知,在球运动轨迹法线方向上有:T2-mgcosθ-F′sinθ=0,解得:T2=mg,故选项C正确;在第二次运动过程中,根据平行四边形定则可知,重力与水平拉力的合力为:
,故选项A正确;此过程中,小球恰能到达Q点,说明vQ=0,根据牛顿第二定律可知,在球运动轨迹法线方向上有:T2-mgcosθ-F′sinθ=0,解得:T2=mg,故选项C正确;在第二次运动过程中,根据平行四边形定则可知,重力与水平拉力的合力为: =mg/cos
=mg/cos ,恒定不变,方向与竖直方向成
,恒定不变,方向与竖直方向成 角,整个过程中小球先加速后减速,当小球运动至轻绳与竖直方向成
角,整个过程中小球先加速后减速,当小球运动至轻绳与竖直方向成 角时,速度最大,根据牛顿第二定律和向心力公式可知,此时轻绳中的拉力亦最大,故选项B错误;在O点、Q点和速度最大点这三点处,重力与水平拉力合力
角时,速度最大,根据牛顿第二定律和向心力公式可知,此时轻绳中的拉力亦最大,故选项B错误;在O点、Q点和速度最大点这三点处,重力与水平拉力合力 的瞬时功率为零,其它位置不为零,因此此过程中
的瞬时功率为零,其它位置不为零,因此此过程中 的功率是先增大后减小,再增大再减小,故选项D错误。
的功率是先增大后减小,再增大再减小,故选项D错误。
考点:本题主要考查了共点力平衡条件、牛顿第二定律、向心力公式、动能定理的应用及瞬时功率的计算问题。

 备战中考寒假系列答案
备战中考寒假系列答案如图所示,蹄形磁铁用柔软的细线悬吊在天花板上,在磁铁两极的正下方固定着一根水平直导线,当直导线通以向右的电流时( )
| A.磁铁的N极向纸外、S极向纸内转动,绳子对磁铁的拉力减小 |
| B.磁铁的S极向纸外、N极向纸内转动,绳子对磁铁的拉力减小 |
| C.磁铁的N极向纸外、S极向纸内转动,绳子对磁铁的拉力增大 |
| D.磁铁的S极向纸外、N极向纸内转动,绳子对磁铁的拉力增大 |
如图所示,位于水平桌面上的木板P,由跨过定滑轮的轻绳与物块Q相连,两段轻绳都是水平的。已知Q与P、 P与桌面之间动摩擦因数均为μ,木板P与物块Q的质量都是m,滑轮的质量、滑轮轴上的摩擦都不计,若用一水平向左的力F拉P使它做匀速运动,则F的大小为( )
| A.3μmg | B.4μmg | C.5μmg | D.6μmg |
如图所示,不计电阻的光滑U形金属框水平放置,光滑、竖直玻璃挡板H、P固定在框上,H、P的间距很小。质量为0.2kg的细金属杆CD恰好无挤压地放在两挡板之间,与金属框接触良好并围成边长为1m的正方形,其有效电阻为0.1Ω。此时在整个空间加方向与水平面成30°角且与金属杆垂直的匀强磁场,磁感应强度随时间变化规律是B =(0.4 -0.2t)T,图示磁场方向为正方向。框、挡板和杆不计形变。则:
| A.t = 1s时,金属杆中感应电流方向从C至D |
| B.t = 3s时,金属杆中感应电流方向从D至C |
| C.t = 1s时,金属杆对挡板P的压力大小为0.1N |
| D.t = 3s时,金属杆对挡板H的压力大小为l.2N |
某大型游乐场内的新型滑梯可以等效为如图所示的物理模型,一个小朋友在AB段的动摩擦因数μ1<tanθ,BC段的动摩擦因数μ2>tanθ,他从A点开始下滑,滑到C点恰好静止,整个过程中滑梯保持静止状态.则该小朋友从斜面顶端A点滑到底端C点的过程中( )
| A.地面对滑梯的摩擦力方向先水平向左,后水平向右 |
| B.地面对滑梯始终无摩擦力作用 |
| C.地面对滑梯的支持力的大小始终等于小朋友和滑梯的总重力的大小 |
| D.地面对滑梯的支持力的大小先大于、后小于小朋友和滑梯的总重力的大小 |
如图所示,轻绳的两端分别系在圆环A和小球B上,圆环A套在粗糙的水平直杆MN上。现用水平力F拉着绳子上的一点O,使小球B从图中实线位置缓慢上升到虚线位置,但圆环A始终保持在原位置不动。则在这一过程中,环对杆的摩擦力Ff和环对杆的压力FN的变化情况是( )
| A.Ff不变,FN不变 |
| B.Ff增大,FN不变 |
| C.Ff增大,FN减小 |
| D.Ff不变,FN减小 |


 =0.5。现有一水平推力F作用于物体B上使B缓慢地向墙壁移动,当移动0.5m时,水平推力的大小为(最大静摩擦力等于滑动摩擦力,g取10 m/s2)
=0.5。现有一水平推力F作用于物体B上使B缓慢地向墙壁移动,当移动0.5m时,水平推力的大小为(最大静摩擦力等于滑动摩擦力,g取10 m/s2)