题目内容
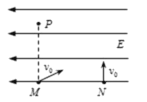
【题目】如图所示，在矩形区域内有垂直于纸面向外的匀强磁场，磁感应强度的大小为B＝5.0×10－2 T，矩形区域长为1.0 m，宽为0.2 m．在AD边中点O处有一放射源，某时刻，放射源沿纸面向磁场中各方向均匀地辐射出速率均为v＝2×106 m/s的某种带正电粒子．已知带电粒子的质量m＝1.6×10－27 kg，所带电荷量为q＝3.2×10－19 C(不计粒子重力)．
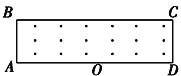
(1)求粒子在磁场中做圆周运动的半径为多大？
(2)求从BC边界射出的粒子，在磁场中运动的最短时间为多少？
【答案】（1）0.2 m.（2）
×10－7 s.
【解析】（1）粒子在磁场中做匀速圆周运动，由牛顿第二定律得： 
，
解得：R=0.2m；
（2）因为所有粒子的轨迹半径相同，所以弦最短的圆所对应的圆心角最小，运动时间最短，作EO⊥AD，EO弦最短，如图所示：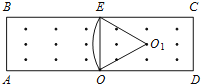
因为EO=0.2m，且R=0.2m，
所以对应的圆心角为θ=
，
由牛顿第二定律得：qvB=m（
）2R，
解得： 
最短时间为： 
，
解得：t=
×10-7s；
练习册系列答案
相关题目
