题目内容
20. 某星球的半径为R,在该星球表面某一倾角为θ的山坡上以初速度v0平抛一物体,经过时间t该物体落到山坡上.(不计一切阻力)
某星球的半径为R,在该星球表面某一倾角为θ的山坡上以初速度v0平抛一物体,经过时间t该物体落到山坡上.(不计一切阻力)(1)该星球表面重力加速度多大?
(2)为了测该星球的自转周期,从该星球发射一颗同步卫星,已知同步卫星离该星球表面高度为h,求该星球的自转周期.
分析 (1)物体做平抛运动,应用平抛运动规律可以求出重力加速度.
(2)卫星绕星球做圆周运动,万有引力提供向心力,由牛顿第二定律求出同步卫星的周期,即星球自转的周期.
解答 解:(1)物体做平抛运动,
水平方向:x=v0t,
竖直方向:y=$\frac{1}{2}$gt2,
由几何关系可知:tanθ=$\frac{y}{x}$=$\frac{gt}{2{v}_{0}}$,
解得:g=$\frac{2{v}_{0}}{t}$tanθ;
(2)星球表面的物体受到的重力等于万有引力,即:G$\frac{Mm}{{R}^{2}}$=mg,
同步卫星做圆周运动,万有引力提供向心力,
由牛顿第二定律得:G$\frac{Mm}{(R+h)^{2}}$=m$(\frac{2π}{T})^{2}$(R+h),
解得:T=2π$\sqrt{\frac{(R+h)^{3}t}{2{v}_{0}{R}^{2}tanθ}}$;
答:(1)该星球表面重力加速度为$\frac{2{v}_{0}}{t}$tanθ;
(2)该星球的自转周期为2π$\sqrt{\frac{(R+h)^{3}t}{2{v}_{0}{R}^{2}tanθ}}$.
点评 本题是一道万有引力定律应用与运动学相结合的综合题,考查了求重力加速度、星球自转的周期,应用平抛运动规律与万有引力公式、牛顿第二定律可以解题;解题时要注意“黄金代换”的应用.

练习册系列答案
相关题目
10. 如图甲所示,一列机械波沿直线ab向右传播,ab=2m,a、b两点的振动情况如图乙所示,下列说法正确的是 ( )
如图甲所示,一列机械波沿直线ab向右传播,ab=2m,a、b两点的振动情况如图乙所示,下列说法正确的是 ( )
 如图甲所示,一列机械波沿直线ab向右传播,ab=2m,a、b两点的振动情况如图乙所示,下列说法正确的是 ( )
如图甲所示,一列机械波沿直线ab向右传播,ab=2m,a、b两点的振动情况如图乙所示,下列说法正确的是 ( )| A. | 波速可能是$\frac{2}{43}$m/s | B. | 波长可能是$\frac{8}{3}$m | ||
| C. | 波速可能是$\frac{3}{7}$m/s | D. | 波速可能是$\frac{2}{7}$m/s | ||
| E. | 波长可能大于$\frac{8}{3}$m |
11.在做完“探究力的平行四边形定则”实验后,某同学将其实验操作过程进行了回顾,并在笔记本上记下如下几条体会,你认为正确的是( )
| A. | 用两只弹簧测力计拉橡皮条时,应使两细绳套间夹角为90°,以便计算合力大小 | |
| B. | 若二力合力的图示F与用一只弹簧测力计拉时图示F′不完全重合,则在误差允许范围内可以说明“力的平行四边形定则”成立 | |
| C. | 若F1、F2方向不变,而大小各增加1N,则合力的方向也不变,大小也增加1N | |
| D. | 在用弹簧测力计拉橡皮条时,要使弹簧测力计的弹簧与木板平面平行 |
8.在科学的发展历程中,许多科学家做出了杰出的贡献.下列叙述符合物理学史实的是( )
| A. | 开普勒以行星运动定律为基础总结出万有引力定律 | |
| B. | 卡文迪许通过实验测出了万有引力常量 | |
| C. | 牛顿提出了万有引力定律,并通过实验测出了万有引力常量 | |
| D. | 伽利略在前人的基础上通过观察总结得到行星运动三定律 |
5. 如图所示,在带有活塞的有机玻璃筒底放置少量硝化棉,迅速压下活塞,观察到硝化棉燃烧起来.关于这个实验,以下说法正确的是( )
如图所示,在带有活塞的有机玻璃筒底放置少量硝化棉,迅速压下活塞,观察到硝化棉燃烧起来.关于这个实验,以下说法正确的是( )
 如图所示,在带有活塞的有机玻璃筒底放置少量硝化棉,迅速压下活塞,观察到硝化棉燃烧起来.关于这个实验,以下说法正确的是( )
如图所示,在带有活塞的有机玻璃筒底放置少量硝化棉,迅速压下活塞,观察到硝化棉燃烧起来.关于这个实验,以下说法正确的是( )| A. | 实验时若是缓慢压下活塞,也能观察到硝化棉燃烧起来 | |
| B. | 玻璃筒内气体的温度升高,筒内气体分子热运动的速率有可能减小 | |
| C. | 硝化棉能燃烧起来,表明气体从外界吸热,内能增加 | |
| D. | 外界对气体做功等于气体向外传递的热量 |
12.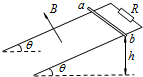 如图所示,一对足够长的光滑平行金属轨道,其轨道平面与水平面成θ角,上端用一电阻R相连,处于方向垂直轨道平面向上的匀强磁场中.质量为m、电阻为r的金属杆ab,从高为h处由静止释放,下滑一段时间后,金属杆开始以速度v匀速运动直到轨道的底端.金属杆始终保持与导轨垂直且接触良好,轨道电阻及空气阻力均可忽略不计,重力加速度为g.则( )
如图所示,一对足够长的光滑平行金属轨道,其轨道平面与水平面成θ角,上端用一电阻R相连,处于方向垂直轨道平面向上的匀强磁场中.质量为m、电阻为r的金属杆ab,从高为h处由静止释放,下滑一段时间后,金属杆开始以速度v匀速运动直到轨道的底端.金属杆始终保持与导轨垂直且接触良好,轨道电阻及空气阻力均可忽略不计,重力加速度为g.则( )
 如图所示,一对足够长的光滑平行金属轨道,其轨道平面与水平面成θ角,上端用一电阻R相连,处于方向垂直轨道平面向上的匀强磁场中.质量为m、电阻为r的金属杆ab,从高为h处由静止释放,下滑一段时间后,金属杆开始以速度v匀速运动直到轨道的底端.金属杆始终保持与导轨垂直且接触良好,轨道电阻及空气阻力均可忽略不计,重力加速度为g.则( )
如图所示,一对足够长的光滑平行金属轨道,其轨道平面与水平面成θ角,上端用一电阻R相连,处于方向垂直轨道平面向上的匀强磁场中.质量为m、电阻为r的金属杆ab,从高为h处由静止释放,下滑一段时间后,金属杆开始以速度v匀速运动直到轨道的底端.金属杆始终保持与导轨垂直且接触良好,轨道电阻及空气阻力均可忽略不计,重力加速度为g.则( )| A. | 金属杆加速运动过程中的平均速度小于$\frac{v}{2}$ | |
| B. | 金属杆加速运动过程中重力做功的功率大于克服安培力做功的功率 | |
| C. | 当金属杆的速度为$\frac{v}{4}$时的加速度大小是速度为$\frac{v}{2}$时加速度大小的2倍 | |
| D. | 整个运动过程中金属杆损失的机械能等于电阻R产生的焦耳热 |
9.“弹弹子”是我国传统的儿童游戏,如图所示,静置于水平地面的两个完全相同的弹子沿一直线排列,质量均为m,人在极短时间内给第一个弹子水平冲量I使其水平向右运动,当第一个弹子运动了距离L时与第二个弹子相碰,碰后第二个弹子运动了距离L时停止.已知摩擦阻力大小恒为弹子所受重力的k倍,重力加速度为g,若弹子之间碰撞时间极短,为弹性碰撞,忽略空气阻力,则人给第一个弹子水平冲量I为( )

| A. | m$\sqrt{6kgL}$ | B. | m$\sqrt{4kgL}$ | C. | m$\sqrt{2kgL}$ | D. | m$\sqrt{kgL}$ |
10. 示波器的工作原理图如图所示,在某一工作状态下,亮点出现在荧光屏上第一象限中的P点;要使亮点水平移动到第二象限中,不能单独采取的措施有( )
示波器的工作原理图如图所示,在某一工作状态下,亮点出现在荧光屏上第一象限中的P点;要使亮点水平移动到第二象限中,不能单独采取的措施有( )
 示波器的工作原理图如图所示,在某一工作状态下,亮点出现在荧光屏上第一象限中的P点;要使亮点水平移动到第二象限中,不能单独采取的措施有( )
示波器的工作原理图如图所示,在某一工作状态下,亮点出现在荧光屏上第一象限中的P点;要使亮点水平移动到第二象限中,不能单独采取的措施有( )| A. | 减小UXX | B. | 增大UXX | ||
| C. | 增大电子枪的加速电压 | D. | 减小电子枪的加速电压 |
 如图所示,ABC为一固定的半圆形轨道,轨道半径R=0.4m,A、C 两点在同一水平面上,B点为轨道最低点.现从A点正上方h=2m的地方以v0=4m/s的初速度竖直向下抛出一质量m=2kg的小球(可视为质点),小球刚好从A点切入半圆轨道.不计空气阻力,取g=10m/s2.
如图所示,ABC为一固定的半圆形轨道,轨道半径R=0.4m,A、C 两点在同一水平面上,B点为轨道最低点.现从A点正上方h=2m的地方以v0=4m/s的初速度竖直向下抛出一质量m=2kg的小球(可视为质点),小球刚好从A点切入半圆轨道.不计空气阻力,取g=10m/s2.