Question

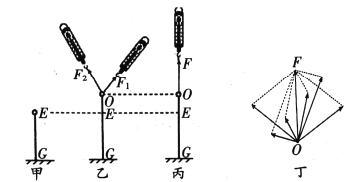
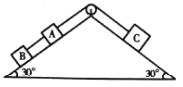
【题目】如图，放置于水平面上的楔形物体，两侧倾角均为30°，左右两表面光滑且足够长，上端固定一光滑滑轮，一根很长且不可伸长的轻绳跨过定滑轮分别与左右两侧斜面平行，绳上系着三个物体A、B、C，三物体组成的系统保持静止.A物体质量为m，B物体质量为3m，现突然剪断A物体和B物体之间的绳子，不计空气阻力(重力加速度为g)，三物体均可视为质点，则

A.绳剪断瞬间，A物体的加速度为

B.绳剪断瞬间，C物体的加速度为

C.绳剪断瞬间，楔形物体对地面的压力不变

D.绳剪断瞬间，A、C间绳的拉力为2mg

Answer 1

【答案】A

【解析】

ABD．设C的质量为m′．绳剪断前，由平衡条件知：

（3m+m）gsin30°=m′gsin30°

得

m′=4m

绳剪断瞬间，以A为研究对象，根据牛顿第二定律得：

T-mgsin30°=ma

以C为研究对象，根据牛顿第二定律得：

4mgsin30°-T=4ma

联立解得：

即绳剪断瞬间，A、C物体的加速度大小均为，A、C间绳的拉力为，故A正确，BD错误。

C．绳剪断前，A、C间绳的拉力为：

T′=（3m+m）gsin30°=2mg

绳剪断瞬间，A、C间绳的拉力为，则AC间绳对定滑轮的压力发生改变，而三个物体对楔形物体的压力不变，可知，绳剪断瞬间，楔形物体对地面的压力发生变化，故C错误。