Question

【题目】如图所示,竖直平面内的空间中,有沿水平方向、垂直于纸面向外的匀强磁场,磁感应强度大小为B,在磁场中建立竖直的平面直角坐标系xOy,在x<0的区域内有沿x轴负向的匀强电场,电场强度大小为E,在x>0的区域内也存在匀强电场（图中未画出）。一个带正电的小球（可视为质点）从x轴上的N点竖直向下做匀速圆周运动至P点后进入x<0的区域,沿着与水平方向成α=30°角斜向上做直线运动,通过x轴上的M点,求:（重力加速度为g,不计空气阻力）

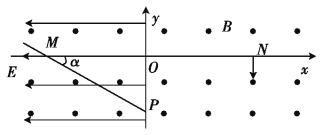
（1）小球运动速度的大小。

（2）在x>0的区域内所加的电场强度的大小。

（3）小球从N点运动到M点所用的时间。

Answer 1

【答案】（1）（2）E （3）

【解析】

试题分析：（1）带电小球做直线运动时的受力情况如图所示

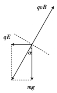
由受力图得qE=mgtan 30°

mg=qvBcos 30°

联立得

（2）小球在x > 0的区域内做匀速圆周运动,则带电小球所受电场力应与所受重力相平衡

qE1=mg

解得E1=E

（3）小球的运动轨迹如图2所示,由几何关系可知∠OPO'=α=30°,∠NO'P=120°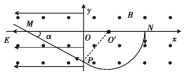

由匀速圆周运动特点,可知小球做圆周运动的半径

由几何知识可知,线段

带电小球做直线运动的时间

带电小球做圆周运动的周期

所以小球做圆周运动从N到P所用的时间

则带电小球从N点到M 点所用的时间t=t1+t2=。