题目内容
1.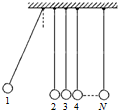 如图所示,用轻绳将大小相同、质量不等的N个小球并列悬挂于一水平杆上,球间有微小间隔,从左到右,球的编号依次为1、2、3 …N,球的质量依次递减,每球质量与其相邻左侧球的质量之比为k(k<1).将1号球向左拉起,然后由静止释放,使其与2号球碰撞,2号球再与3号球碰撞 …所有碰撞均为无机械能损失的正碰.(不计空气阻力)
如图所示,用轻绳将大小相同、质量不等的N个小球并列悬挂于一水平杆上,球间有微小间隔,从左到右,球的编号依次为1、2、3 …N,球的质量依次递减,每球质量与其相邻左侧球的质量之比为k(k<1).将1号球向左拉起,然后由静止释放,使其与2号球碰撞,2号球再与3号球碰撞 …所有碰撞均为无机械能损失的正碰.(不计空气阻力)(i)求n号球与n+1号球碰撞后的速率之比;
(ii)若N=5,k=$\sqrt{2}$-1,在1号球向左拉高h(远小于绳长)的情况下,问5号球碰撞后上升的最大高度.
分析 (1)根据动量守恒定律和能量守恒定律求出n号球与n+1号球碰撞后的速率之比;
(2)根据动能定理,以及碰后n+1号球与碰前号球的速度关系得出通项表达式,结合动能定理求出5号球碰撞后上升的最大高度.
解答 解:(i)规定向右为正方向,根据动量守恒定律得,mnvn=mnvn′+kmnvn+1′,
根据能量守恒得,$\frac{1}{2}{m}_{n}{{v}_{n}}^{2}=\frac{1}{2}{m}_{n}{v}_{n}{′}^{2}+\frac{1}{2}k{m}_{n}{v}_{n+1}{′}^{2}$,
联立解得$\frac{{v}_{n}′}{{v}_{n+1}′}=\frac{1-k}{2}$.
$\frac{{v}_{n+1}′}{{v}_{n}}=\frac{2}{k+1}$
(ii)根据动能定理得,${m}_{1}gh=\frac{1}{2}{m}_{1}{{v}_{1}}^{2}$,
根据归纳法知,${v}_{5}′=(\frac{2}{1+k})^{4}{v}_{1}$,
根据动能定理有:${m}_{5}gh′=\frac{1}{2}{m}_{5}{v}_{5}{′}^{2}$,
解得h′=16h.
答:(i)n号球与n+1号球碰撞后的速率之比为$\frac{1-k}{2}$;(ii)5号球碰撞后上升的最大高度为16h.
点评 本题是利用动量守恒和机械能守恒联合解决一维碰撞问题的典型例子,其中由1号球的速度归纳第n+1号球的速度是关键,而且也是难点.

练习册系列答案
相关题目
9.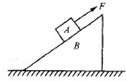 如图所示,斜面体B放在水平地面上,木块A放在斜面体B上,用一个沿斜面向上的力F拉木块A,在力F的作用下,物体A与斜面体B一起沿水平方向匀速移动,已知斜面倾角为θ,则关于斜面体B受力的个数,下面说法中正确的是( )
如图所示,斜面体B放在水平地面上,木块A放在斜面体B上,用一个沿斜面向上的力F拉木块A,在力F的作用下,物体A与斜面体B一起沿水平方向匀速移动,已知斜面倾角为θ,则关于斜面体B受力的个数,下面说法中正确的是( )
 如图所示,斜面体B放在水平地面上,木块A放在斜面体B上,用一个沿斜面向上的力F拉木块A,在力F的作用下,物体A与斜面体B一起沿水平方向匀速移动,已知斜面倾角为θ,则关于斜面体B受力的个数,下面说法中正确的是( )
如图所示,斜面体B放在水平地面上,木块A放在斜面体B上,用一个沿斜面向上的力F拉木块A,在力F的作用下,物体A与斜面体B一起沿水平方向匀速移动,已知斜面倾角为θ,则关于斜面体B受力的个数,下面说法中正确的是( )| A. | 可能是3个 | B. | 可能是4个 | C. | 可能是5个 | D. | 一定是5个 |
16.关于天然放射现象,叙述正确的是( )
| A. | 若使放射性物质与其他物质发生化学反应,其半衰期不会改变 | |
| B. | β衰变所释放的电子不可能是原子核外的电子电离形成的 | |
| C. | 在α、β、γ这三种射线中,γ射线的穿透能力最强,α射线的电离能力最强 | |
| D. | 铀核(${\;}_{92}^{238}$U)衰变为铅核(${\;}_{82}^{206}$Pb)的过程中,要经过8次α衰变和10次β衰变 |
13.火车轨道在转弯处外轨高于内轨,其高度差由转弯半径与火车速度确定.若在某转弯处规定行驶的速度为v,则下列说法中错误的是( )
| A. | 当速度大于v时,轮缘挤压外轨 | |
| B. | 当速度小于v时,轮缘挤压内轨 | |
| C. | 当以v的速度通过此弯路时,轮缘既不挤压外轨,也不挤压内轨 | |
| D. | 当以v的速度通过此弯路时,火车受到的重力与轨道对火车的支持力是一对平衡力 |
10.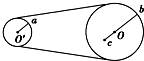 如图所示的皮带传动中,小轮半径ra是大轮半径rb的一半,大轮上c点到轮心O的距离恰等于ra,若皮带不打滑,则图中a、b、c三点( )
如图所示的皮带传动中,小轮半径ra是大轮半径rb的一半,大轮上c点到轮心O的距离恰等于ra,若皮带不打滑,则图中a、b、c三点( )
 如图所示的皮带传动中,小轮半径ra是大轮半径rb的一半,大轮上c点到轮心O的距离恰等于ra,若皮带不打滑,则图中a、b、c三点( )
如图所示的皮带传动中,小轮半径ra是大轮半径rb的一半,大轮上c点到轮心O的距离恰等于ra,若皮带不打滑,则图中a、b、c三点( )| A. | 线速度之比为2:1:1 | B. | 角速度之比为2:1:1 | ||
| C. | 转动周期之比为2:1:1 | D. | 向心加速度大小之比为4:2:1 |
 如图,在0≤x≤$\sqrt{3}$a区域内存在与xy平面垂直的匀强磁场,磁感强强度的大小为B.在t=0时刻,一位于坐标原点的粒子源在xy平面内发射出大量同种带电粒子,所有粒子的初速度大小相同,方向与y轴正方向的夹角分布在0-180°范围内.已知沿y轴正方向发射的粒子在t=t0时刻刚好从磁场边界上P($\sqrt{3}$a,a)点离开磁场.求:
如图,在0≤x≤$\sqrt{3}$a区域内存在与xy平面垂直的匀强磁场,磁感强强度的大小为B.在t=0时刻,一位于坐标原点的粒子源在xy平面内发射出大量同种带电粒子,所有粒子的初速度大小相同,方向与y轴正方向的夹角分布在0-180°范围内.已知沿y轴正方向发射的粒子在t=t0时刻刚好从磁场边界上P($\sqrt{3}$a,a)点离开磁场.求: 做描绘小灯泡L的伏安特性曲线实验,已知该灯泡的额定电流为0.5A,最大阻值约为9Ω.提供的备用器材有:
做描绘小灯泡L的伏安特性曲线实验,已知该灯泡的额定电流为0.5A,最大阻值约为9Ω.提供的备用器材有: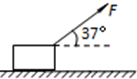 如图所示,水平地面上有一质量m=2.3kg的金属块,其与水平地面间的动摩擦因数μ=0.2.在与水平方向成θ=37°角斜向上的拉力F作用下,以v=2m/s的速度向右做匀速直线运动.已知sin37°=0.6,cos37°=0.8,g取10m/s2.求:
如图所示,水平地面上有一质量m=2.3kg的金属块,其与水平地面间的动摩擦因数μ=0.2.在与水平方向成θ=37°角斜向上的拉力F作用下,以v=2m/s的速度向右做匀速直线运动.已知sin37°=0.6,cos37°=0.8,g取10m/s2.求: