题目内容
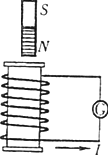
如图所示,螺线管与相距L的两竖直放置的导轨相连,导轨处于垂直纸面向外、磁感应强度为B0的匀强磁场中.金属杆ab垂直导轨,杆与导轨接触良好,并可沿导轨无摩擦滑动.螺线管横截面积为S,线圈匝数为N,电阻为R1,管内有水平向左的变化磁场.已知金属杆ab的质量为m,电阻为R2,重力加速度为g.不计导轨的电阻,不计空气阻力,忽略螺线管磁场对杆ab的影响.
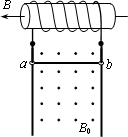
(1)为使ab杆保持静止,求通过ab的电流的大小和方向;
(2)当ab杆保持静止时,求螺线管内磁场的磁感应强度B的变化率;
(3)若螺线管内方向向左的磁场的磁感应强度的变化率![]() (k>0).将金属杆ab由静止释放,杆将向下运动.当杆的速度为v时,仍在向下做加速运动.求此时杆的加速度的大小.设导轨足够长.
(k>0).将金属杆ab由静止释放,杆将向下运动.当杆的速度为v时,仍在向下做加速运动.求此时杆的加速度的大小.设导轨足够长.
答案:
解析:
解析:
|
解:(1)以ab为研究对象,根据平衡条件 mg=B0IL (2分) 求出 通过ab杆电流方向为由b到a(或在图中标出) (2分) (2)根据法拉第电磁感应定律 根据欧姆定律 求出 (3)根据法拉第电磁感应定律 ab杆切割磁感线产生的电动势E2=B0Lv (1分) 总电动势 E总=E1+E2 (1分) 感应电流 根据牛顿第二定律 安培力 F=B0 求出 |

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
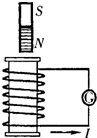
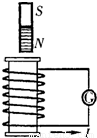
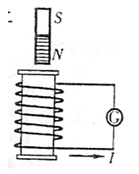
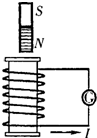 如图所示,螺线管与电流表组成闭合电路,条形磁铁位于螺线管上方,下端为N极.则当螺线管中产生的感应电流( )
如图所示,螺线管与电流表组成闭合电路,条形磁铁位于螺线管上方,下端为N极.则当螺线管中产生的感应电流( )