Question

17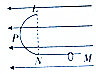．如图所示，在E=75V/m的水平方向的匀强电场中，有一光滑的半圆形绝缘轨道LPN与一水平绝缘轨道MN连接，半圆形所在的竖直平面与电场线平行，其半径R=0.40m．其中P为LN圆弧的中点，直径LN与水平轨道MN垂直，另有一个带正电荷量q=1×10^-3C，质量m=1.0×10^-2kg的小环套在轨道上，此环自位于N点右侧x=1.2m处以初速度v₀向左开始运动，已知小环与水平轨道间的动摩擦因数μ=0.25，且它恰能运动到圆轨道的最高点L，取g=10m/s² ，求：
（1）小环的初速度v₀．
（2）小环第一次通过P点时对轨道的压力大小．
（3）小环在运动过程中的最大动能．

Answer 1

分析 （1）在小滑块运动的过程中，摩擦力对滑块和重力做负功，电场力对滑块做正功，根据动能定理可以求得滑块初速度；
（2）在P点时，对滑块受力分析，由牛顿第二定律可以求得滑块受到的轨道对滑块的支持力的大小，由牛顿第三定律可以求滑块得对轨道压力
（3）由于qE＞μmg，所以物体先做匀加速直线运动，到达N后电场力做正功，重力做负功，最大速度出现在电场力与重力的合力位置处的圆弧轨道处

解答 解：（1）滑块从开始运动到达L的过程中，由动能定理得：
qEx-2mgR-μmgx=$\frac{1}{2}$mv²-$\frac{1}{2}m$${v}_{0}^{2}$，
滑块恰能达到最高点，重力提供向心力，由牛顿第二定律得：mg=m$\frac{{V}^{2}}{R}$，
代入数据解得：V₀=2m/s；
（2）设滑块在P点的速度为v₁，由动能定理得：
qE（x+R）-mgR-μmgx=$\frac{1}{2}$mv₁²-$\frac{1}{2}m$${v}_{0}^{2}$，
设滑块在P点所受的压力为N，由牛顿第二定律得：
N-qE=m$\frac{{V}_{1}^{2}}{R}$，
解得：N=0.525N，由牛顿第三定律可知，
滑块通过P点时对轨道的压力大小为0.525N；
（3）由于qE＞μmg，所以物体先做匀加速直线运动，到达N后电场力做正功，重力做负功，最大速度出现在电场力与重力的合力位置处的圆弧轨道处，其合力与重力方向成$tanθ=\frac{qE}{mg}=3$．
设小球的最大动能为E_km，依据动能定理
qE（x+Rsinθ）-mgR（1-cosθ）-μmgx=E_km-$\frac{1}{2}m$${v}_{0}^{2}$，
解得E_km=0.053J
答：（1）小环的初速度2m/s；
（2）小环第一次通过P点时对轨道的压力大小0.525N．
（3）小环在运动过程中的最大动能0.053J

点评 本题中涉及到的物体的运动的过程较多，对于不同的过程要注意力做功数值的不同，特别是恰好通过最高点时解题的突破口，滑块的运动状态的分析是本题中的难点，一定要学会分不同的方向来分析和处理问题