题目内容
甲、乙两处相距8m.物体A由甲处向乙处的方向作匀加速直线运动,初速度为零,加速度为2m/s2;物体B由乙处出发沿A运动的同一方向作匀速直线运动,速度是4m/s,但比A早1s钟开始运动.求:
(1)物体A开始运动后经多少时间追上物体B?
(2)物体A开始运动后经多少时间两物相距最远?这个最远距离是多大?
解:设甲、乙两处相距l0,则l0=8m
(1)假设A开始运动后经过时间t追上:
对A:由匀变速直线运动的规律得:
xA= =
=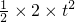 =t2
=t2
对B:匀速直线运动:
xB=vt=4×(t+1)
相遇时:
xA-l0=xB
即:t2-8=4t+4
解得:t=6s或-2s(-2s不符合题意舍去)
所以:t=6s
(2)当A、B两物体速度相等都等于4m/s时,两物体相距最远,
对A:由匀变速直线运动的规律得:
v=at,即:4=2×t,解得:t=2s
A的位移为:xA= =2×2=4m
=2×2=4m
B的位移为:xB=v×(t+1)=4×3=12m
所以相距最大值为:xB+l0-xA=12+8-4=16m
答:(1)物体A开始运动后经6s追上物体B.
(2)物体A开始运动后2s两物相距最远.这个最远距离是16m
分析:本题是匀变速运动中的追及相遇问题,物体A追上物体B说明A、B两物体位移相等,列式找关系即可,匀加速追赶匀速,速度相等时距离是最大的.抓住位移相等和速度关系这两点列式求解即可.
点评:本题是匀变速运动中的追及相遇问题,抓住时间关系,位移关系,速度关系这三个关键点结合匀变速直线运动的规律列式求解即可.
(1)假设A开始运动后经过时间t追上:
对A:由匀变速直线运动的规律得:
xA=
 =
=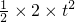 =t2
=t2对B:匀速直线运动:
xB=vt=4×(t+1)
相遇时:
xA-l0=xB
即:t2-8=4t+4
解得:t=6s或-2s(-2s不符合题意舍去)
所以:t=6s
(2)当A、B两物体速度相等都等于4m/s时,两物体相距最远,
对A:由匀变速直线运动的规律得:
v=at,即:4=2×t,解得:t=2s
A的位移为:xA=
 =2×2=4m
=2×2=4mB的位移为:xB=v×(t+1)=4×3=12m
所以相距最大值为:xB+l0-xA=12+8-4=16m
答:(1)物体A开始运动后经6s追上物体B.
(2)物体A开始运动后2s两物相距最远.这个最远距离是16m
分析:本题是匀变速运动中的追及相遇问题,物体A追上物体B说明A、B两物体位移相等,列式找关系即可,匀加速追赶匀速,速度相等时距离是最大的.抓住位移相等和速度关系这两点列式求解即可.
点评:本题是匀变速运动中的追及相遇问题,抓住时间关系,位移关系,速度关系这三个关键点结合匀变速直线运动的规律列式求解即可.

练习册系列答案
相关题目