Question

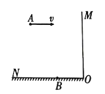
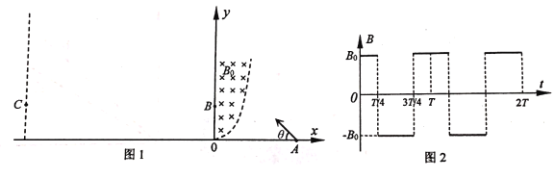
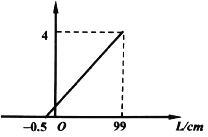
【题目】如图1所示为平面坐标系，在第一象限内的虚曲线和轴之间存在着垂直纸面向里的匀强磁场，磁感应强度大小为；在第二象限内的虚直线（）和轴之间存在着如图2所示的交变磁场（以垂直纸面向外为磁场的正方向）．在（，）点的放射源发出质量为、带电量为的粒子，粒子速度大小为，速度方向与轴负方向的夹角为（），所有粒子都能垂直穿过轴后进入第二象限．不计粒子重力和粒子间相互作用．

(1)求夹角的粒子经过轴时的坐标；

(2)求第一象限内虚曲线的曲线方程；

(3)假设交变磁场在时刻，某粒子刚好经过轴上的（，）点，则

①要求该粒子不回到第一象限，交变磁场的变化周期T应满足什么条件？

②要求该粒子在（，）点垂直虚直线水平射出磁场，求粒子在交变磁场中运动时间与磁场变化周期的比值的最小值？并求出在这种情况下粒子在交变磁场中的运动时间．

Answer 1

【答案】(1)；(2)；(3)①；②

【解析】

（1）粒子在磁场中做匀速圆周运动，轨迹半径为，则：

解得：

，

如图1所示，

当入射角为时，根据几何关系可得：y轴坐标

（2）如图2所示，入射角为任意角，进入磁场入射点坐标为（，），

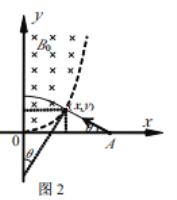
根据几何关系可得：

得

（）

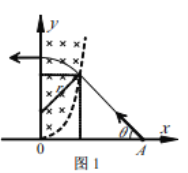
（3）①粒子不回到第一象限，临界情况为轨迹与轴相切，如图3所示；

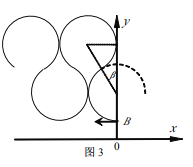
设粒子在磁场中运动的周期为，两圆心连线与轴夹角为，则：

所以

且满足

得

要求该粒子不回到第一象限，交变磁场的变化周期应满足

；

②粒子在交变磁场中运动的时间与磁场变化的周期的比值为，即

如图4所示

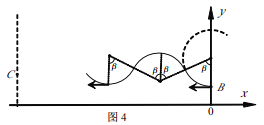
根据几何关系可得：

由于，所以最小等于，即

当，如图4所示，粒子运动时间

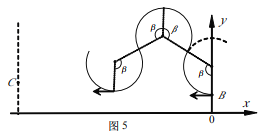
当β=120°时，如图5所示，粒子运动时间