��Ŀ����
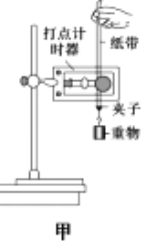
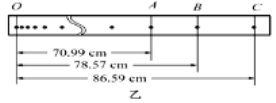
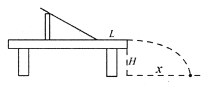
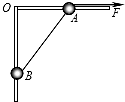
����Ŀ����ͼ��ʾ����ֱƽ���ڷ�һֱ�Ǹ�AOB���˵�ˮƽ���ֲִڣ���Ħ��������=0��2���˵���ֱ���ֹ⻬�������ָ���������Ϊ1kg��С��A��B��A��B����ϸ����������ʱA��B���ھ�ֹ״̬��OA=3m��OB=4m������ˮƽ����F���һ�������Aʹ֮�ƶ�1m�������������ٶ�g=10m/s2����
��1���ù�����A�ܵ���Ħ�����������F�������٣�
��2������20N�ĺ�����A��Ҳ�ƶ�1m����ʱA���ٶȴﵽ2m/s����˹����в���������Ϊ���٣�
���𰸡���1��4N��14J ��2��4��4J
��������
�����������1����AB��������������������F������G��֧����N�������Ħ����f�����ҵĵ���N1����ͼ
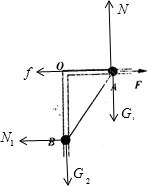
���ݹ�����ƽ����������
��ֱ����N=G1+G2
ˮƽ����F=f+N1
����f=��N
���N=��m1+m2��g=20N
f=��N=0��2��20N=4N
�������������˶����������ö��ܶ�����ʽ���õ�WF��fs��m2gh=0
���ݼ��ι�ϵ����֪��B��������h=1m����WF=fs+m2gh=4��1+1��10��1=14J
��2�����ݹ��ܹ�ϵ֪��FS=![]() mvA2+
mvA2+![]() mvB2+E��+mgh��
mvB2+E��+mgh��
�����ٶȵķֽ���ϳ�֪B���ٶ�Ϊ![]() m/s
m/s
���E��=20��1��0��5��1��4��0��5��1��![]() ��1��10��1=4��4J
��1��10��1=4��4J