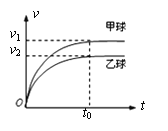
题目内容
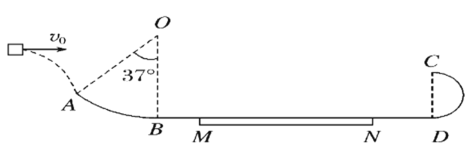
【题目】如图所示,质量m=0.3kg的小物块以初速度v0=4m/s水平向右抛出,恰好从A点沿着圆弧的切线方向进入光滑圆弧轨道.圆弧轨道的半径为R=3.75m,B点是圆弧轨道的最低点,圆弧轨道与水平轨道BD平滑连接,A与圆心O的连线与竖直方向成37°角.MN是一段粗糙的水平轨道,小物块与MN间的动摩擦因数μ=0.1,轨道其他部分光滑.最右侧是一个半径为r=0.4 m的光滑半圆弧轨道,C点是半圆弧轨道的最高点,半圆弧轨道与水平轨道BD在D点平滑连接.已知重力加速度g=10 m/s2,sin 37°=0.6,cos 37°=0.8;
(1)求小物块经过A点时速度大小;
(2)求小物块经过B点时对轨道的压力大小;
(3)若小物块恰好能通过C点,求MN的长度L.
【答案】(1)vA=5 m/s (2)6.2 N (3) L′=10m
【解析】
(1)根据平抛运动的规律有
v0=vAcos 37°
得经过A点时的速度大小
vA=5 m/s
(2)小物块从A点到B点,根据机械能守恒定律
![]() +mg(R-Rcos 37°)=
+mg(R-Rcos 37°)=![]()
小物块经过B点时,根据牛顿第二定律有
FN-mg=![]()
解得
FN=6.2 N
根据牛顿第三定律,小物块经过B点时对轨道的压力大小是6.2 N
(3)小物块刚好能通过C点时,根据牛顿第二定律有
mg=![]()
解得
vC′=2 m/s
从B点运动到C点,根据动能定理有
-μmgL′-2mgr=![]() mvC′2-
mvC′2-![]()
解得
L′=10 m

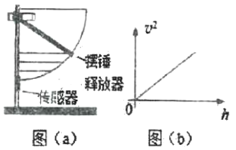
【题目】在“用DIS研究机械能守恒定律"的实验中,某同学将传感器固定在最低点,如图(a)所示。该同学将摆锤从不同位置由静止释放,记录摆锤每次下落的高度h和最低点的速度v,作出了如图(b)所示的v2-h图线,则该直线的斜率应为________________,计算摆锤在释放点和最低点之间的势能变化大小△Ep与动能变化大小△Ek,结果如下列表格所示(重力加速度为g)。
△Ep(×10-2J) | 4.89 | 9.79 | 14.69 | 19.59 | 29.38 |
△Ek(×10-2J) | 5.04 | 10.10 | 15.11 | 20.02 | 29.85 |
结果显示△Ep与△Ek之间存在差异,他认为这并不是由于空气阻力造成的,理由是_________________________。