题目内容
4.2015年春运期间,一乘客由于疏忽,延误了班车.设班车出站后即以20m/s的速度匀速行驶,2分钟后乘客发现立即电话告知班车随车人员,请求班车停车.班车司机立即关闭油门以2m/s2的加速度匀减速前进,打电话1分钟后乘客乘出租车开始追赶班车,出租车与班车同方向以2m/s2的加速度从同一车站出口处出发,由静止开始做匀加速运动,出租车的最大速度为40m/s,则( )| A. | 出租车出发后最快经72.5s追上班车 | |
| B. | 出租车出发后最快经132.5s追上班车 | |
| C. | 出租车追上班车时距离车站2500m | |
| D. | 出租车追上班车时距离车站2400m |
分析 根据速度时间公式求出班车速度减为零的时间,结合速度位移公式求出班车速度减为零的位移,求出班车2min内匀速运动的位移,从而得出出租车追上班车时距离车站的距离.根据速度时间公式求出出租车速度达到最大速度的时间,结合速度位移公式求出达到最大速度的位移,从而得出匀速运动的位移,求出匀速运动的时间,从而得出出租车追及的时间.
解答 解:班车减速到零需要的时间为:${t}_{0}=\frac{{v}_{0}}{{a}_{1}}=\frac{20}{2}s=10s$,
班车减速到零的位移为:${x}_{1}=\frac{{{v}_{0}}^{2}}{2{a}_{1}}=\frac{400}{4}m=100m$,
班车2分钟内匀速运动的位移为:x2=v1t1=20×120m=2400m,
可知出租车追上班车离车站对的距离为:x=x1+x2=100+2400m=2500m.故C正确,D错误.
出租车达到最大速度经历的时间为:${t}_{2}=\frac{{v}_{m}}{{a}_{2}}=\frac{40}{2}s=20s$,
达到最大速度经历的位移为:${x}_{3}=\frac{{{v}_{m}}^{2}}{2{a}_{2}}=\frac{1600}{4}m=400m$,
则匀速运动的时间为:${t}_{3}=\frac{x-{x}_{3}}{{v}_{m}}=\frac{2500-400}{40}s=52.5s$,
则追及的时间为:t=t2+t3=20+52.5s=72.5s,故A正确,B错误.
故选:AC.
点评 本题考查了运动学中的追及问题,求解时注意出租车速度达到最大速度后做匀速运动,以及班车速度减为零后不再运动.

练习册系列答案
相关题目
16.关于加速度的说法中正确的是( )
| A. | 加速度就是速度的增加量 | |
| B. | 加速度是矢量,其方向就是速度的方向 | |
| C. | 加速度越大,物体的速度变化也越大 | |
| D. | 加速度越大,物体的速度变化越快 |


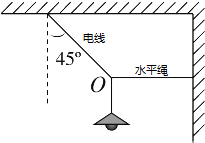 电线上端固定在天花板上,下端吊一盏10N的电灯,为了调节室内照明,用绳子将灯拉至如图所示的位置,求电线和水平绳子的拉力各是多少?(画力图)
电线上端固定在天花板上,下端吊一盏10N的电灯,为了调节室内照明,用绳子将灯拉至如图所示的位置,求电线和水平绳子的拉力各是多少?(画力图) 如图所示,静止在光滑水平面上的斜面体,质量为M,倾角为α,其斜面上有一静止的滑块.质量为m,两者之间的动摩擦因数为μ,滑块受到的最大静摩擦力可认为等于滑动摩擦力,重力加速度为g.现给斜面体施加水平向右的力使斜面体加速运动,求:若要使滑块与斜面体一起加速运动,图中水平向右的力F的最大值.
如图所示,静止在光滑水平面上的斜面体,质量为M,倾角为α,其斜面上有一静止的滑块.质量为m,两者之间的动摩擦因数为μ,滑块受到的最大静摩擦力可认为等于滑动摩擦力,重力加速度为g.现给斜面体施加水平向右的力使斜面体加速运动,求:若要使滑块与斜面体一起加速运动,图中水平向右的力F的最大值.