题目内容
宇宙中有一半径为R的星球,宇航员站在该星球上离星球表面h高处以速度v平行星球表面抛出一质量为m的小球,测得小球的水平位移为x,这一平抛运动的空间范围很小,可不计重力加速度的变化.下列判断正确的是( )
分析:根据平抛运动的规律,求出平抛运动的重力加速度,根据重力提供向心力,求出第一宇宙速度的大小.根据重力提供向心力求出向心加速度的大小和线速度的大小,结合圆周运动的周期公式求出绕该星球表面附近运行的卫星的周期.
解答:解:A、根据h=
gt2,x=vt得,g=
,根据mg=m
,解得v0=
=
,知在该星球表面上以v0=
的初速度水平抛出一物体,物体将不再落回星球.故A错误,B正确.
C、卫星贴近星球表面附近运行,有:mg=ma,解得a=
.故C正确.
D、根据mg=m
,解得v0=
=
,则周期T=
=
.故D错误.
故选BC.
| 1 |
| 2 |
| 2v2h |
| x2 |
| v02 |
| R |
| gR |
| v |
| x |
| 2Rh |
| v |
| x |
| 2Rh |
C、卫星贴近星球表面附近运行,有:mg=ma,解得a=
| 2v2h |
| x2 |
D、根据mg=m
| v02 |
| R |
| gR |
| v |
| x |
| 2Rh |
| 2πR |
| v0 |
| 2πxR | ||
v
|
故选BC.
点评:解决本题的关键知道卫星在星球表面附近所受的万有引力等于重力,结合重力提供向心力进行分析求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

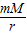 (G为万有引力常量),设宇宙中有一半径为R的星球,宇航员在该星球上以速度v竖直向上抛出一质量为m的物体,不计空气阻力,经t秒后落回手中,则描述正确的是( )
(G为万有引力常量),设宇宙中有一半径为R的星球,宇航员在该星球上以速度v竖直向上抛出一质量为m的物体,不计空气阻力,经t秒后落回手中,则描述正确的是( )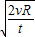 的初速度水平抛出一个物体,物体将不再落回星球表面
的初速度水平抛出一个物体,物体将不再落回星球表面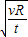 的初速度水平抛出一个物体,物体将不再落回星球表面
的初速度水平抛出一个物体,物体将不再落回星球表面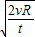 的初速度竖直抛出一个物体,物体将不再落回星球表面
的初速度竖直抛出一个物体,物体将不再落回星球表面 的初速度竖直抛出一个物体,物体将不再落回星球表面
的初速度竖直抛出一个物体,物体将不再落回星球表面