题目内容
 在做“用单摆测定重力加速度”的实验中,
在做“用单摆测定重力加速度”的实验中,(1)某同学用毫米刻度尺测得摆线长L0=949.9mm;用游标卡尺测得 摆球的直径如图甲所示,则摆球直径d=
20.20
20.20
mm;用秒表测得单摆完成n=50次全振动的时间如图乙所示,则秒表的示数t=100.2
100.2
s;写出用本题给定物理量符号表示当地的重力加速度的表达式g=4π2n2(L0+
| ||
| t2 |
4π2n2(L0+
| ||
| t2 |
9.56
9.56
m/s2 (取π2=10 )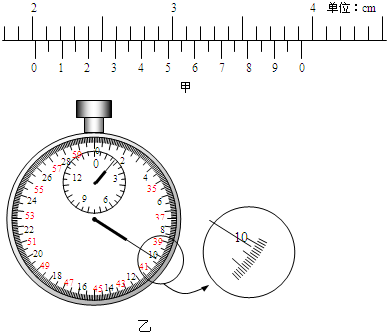
(2)若该同学测得g值偏大,那么可能原因是
BD
BD
(不定项)A.计算摆长时没有计入摆球的半径
B.开始计时时,秒表过迟按下
C.摆线上端未牢固地系于悬点,振动中出现松动,使摆线长度增加了
D.试验中误将39次全振动数为40次
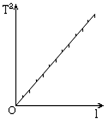
(3)为了提高实验精度,在实验中可改变几次摆长L并测出相应的周期T,从而得出几组对应的L与T的数据,再以L为横坐标,T2为纵坐标将所得数据点连成直线(如图),并求得该直线的斜率为K,则重力加速度g=
| 4π2 |
| k |
| 4π2 |
| k |
分析:考查游标卡尺和秒表的读数:先读主尺(只读整数),再加上游标尺(格数乘以分度分之一,格数找对齐的一个不估读);秒表读数等于大盘刻度读数加上小盘刻度读数;根据单摆周期公式列式分析即可.
解答:解:(1)直径读数:主尺:20mm,游标对其格数:4个格,读数:4×0.05=0.20mm
所以直径为:20+0.20=20.20mm
大表盘读数为:90s
小盘读数为:10.2s
故时间为:90+10.2=100.2s
根据单摆的周期公式T=2π
,可得:g=
=
代入数据得:g=9.56m/s2
(2)根据单摆的周期公式T=2π
,可得:g=
A.计算摆长时没有计入摆球的半径.则摆长偏小,故重力加速度偏小,故A错误
B、秒表过迟按下,导致周期偏小,故重力加速度偏大,故B正确
C、振动中出现松动,但计算时仍用开始测得的值,将导致g偏小,故C错误
D、试验中将39次全振动数为40次,根据T=
,周期偏小,故g偏大,故D正确
故选:BD
(3)由图知,斜率k=
,代入g=
可得:g=
故答案为:(1)20.20 100.2,
9.56
(2)BD (3)
所以直径为:20+0.20=20.20mm
大表盘读数为:90s
小盘读数为:10.2s
故时间为:90+10.2=100.2s
根据单摆的周期公式T=2π
|
| 4π2L |
| T2 |
4π2n2(L0+
| ||
| t2 |
代入数据得:g=9.56m/s2
(2)根据单摆的周期公式T=2π
|
| 4π2L |
| T2 |
A.计算摆长时没有计入摆球的半径.则摆长偏小,故重力加速度偏小,故A错误
B、秒表过迟按下,导致周期偏小,故重力加速度偏大,故B正确
C、振动中出现松动,但计算时仍用开始测得的值,将导致g偏小,故C错误
D、试验中将39次全振动数为40次,根据T=
| t |
| n |
故选:BD
(3)由图知,斜率k=
| T2 |
| L |
| 4π2L |
| T2 |
可得:g=
| 4π2 |
| k |
故答案为:(1)20.20 100.2,
4π2n2(L0+
| ||
| t2 |
(2)BD (3)
| 4π2 |
| k |
点评:本题关键是会读数常用的实验仪器,能结合单摆的周期公式分析误差.

练习册系列答案
相关题目