题目内容
图中实线和虚线分别是x轴上传播的一列简谐横波在t=0和t=0.03 s时刻的波形图,x=1.2 m处的质点在t=0.03 s时刻向y轴正方向运动,则( )


| A.该波的频率可能是125 Hz |
| B.该波的波速可能是10 m/s |
| C.t=0时x=1.4 m处质点的加速度方向沿y轴负方向 |
| D.各质点在0.03 s内随波迁移0.9 m |
AC
考点:
分析:根据两个时刻的波形,得到周期的通项,求出频率的通项,确定特殊值.由波速通项分析特殊值.由t=0.03s时刻向y轴正方向运动判断波的传播方向,分析t=0时x=1.4m处质点的加速度方向和速度方向.
解答:解:A、由题x=1.2m处的质点在t=0.03s时刻向y轴正方向运动,可知波向右传播.则时间△t=(n+ )T,频率f=
)T,频率f=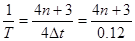 Hz,(n=0,1,2,、、、)当n=3时,f=125Hz.故A正确.
Hz,(n=0,1,2,、、、)当n=3时,f=125Hz.故A正确.
B、波速的通项v="λf=40n+30" m/s,n=0,1,2,、、、,因为n是整数,故v不可能等于10m/s.故B错误.
C、t=0时x=1.4m处质点位于x轴上方,加速度方向沿y轴负方向.故C正确
D、质点不随波迁移.故D错误.
故选AC
点评:本题考查由两个时刻的波形列出通项的能力.考查运用数学知识解决物理问题能力是高考考查的五大能力之一.
分析:根据两个时刻的波形,得到周期的通项,求出频率的通项,确定特殊值.由波速通项分析特殊值.由t=0.03s时刻向y轴正方向运动判断波的传播方向,分析t=0时x=1.4m处质点的加速度方向和速度方向.
解答:解:A、由题x=1.2m处的质点在t=0.03s时刻向y轴正方向运动,可知波向右传播.则时间△t=(n+
 )T,频率f=
)T,频率f=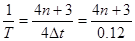 Hz,(n=0,1,2,、、、)当n=3时,f=125Hz.故A正确.
Hz,(n=0,1,2,、、、)当n=3时,f=125Hz.故A正确.B、波速的通项v="λf=40n+30" m/s,n=0,1,2,、、、,因为n是整数,故v不可能等于10m/s.故B错误.
C、t=0时x=1.4m处质点位于x轴上方,加速度方向沿y轴负方向.故C正确
D、质点不随波迁移.故D错误.
故选AC
点评:本题考查由两个时刻的波形列出通项的能力.考查运用数学知识解决物理问题能力是高考考查的五大能力之一.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目





 方向传播, 波速为4.0m/s
方向传播, 波速为4.0m/s



 。一细束光线在纸面内从O点射人棱镜,光线与AB面间的垂线夹角为
。一细束光线在纸面内从O点射人棱镜,光线与AB面间的垂线夹角为 ,通过观察发现此时无光线从AC面射出,有光线垂直于BC面从棱镜射出。稍稍减小
,通过观察发现此时无光线从AC面射出,有光线垂直于BC面从棱镜射出。稍稍减小

 出下列时刻振子对平衡位置的位移.
出下列时刻振子对平衡位置的位移. 5s.
5s.
