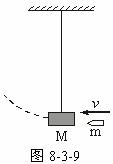
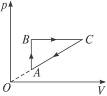
题目内容
如图8-3-9所示,粗细均匀,两端开口的U形管竖直放置,管的内径很小,水平部分BC长14 cm.一空气柱将管内水银分离成左右两段.大气压强相当于高为76 cmHg的压强.
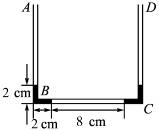
图8-3-9
(1)当空气柱温度为T0=273 K,长为l0=8 cm时,BC管内左边水银柱长2 cm,AB的管内水银柱长是2 cm,则右边水银柱总长是多少?
(2)当空气柱温度升高到多少时,左边的水银恰好全部进入竖直管AB内?
(3)当空气柱温度为490 K时,两竖直管内水银柱上表面高度各为多少?
(1)6 cm (2) 420 K (3)左6 cm 右4 cm
解析:
(1)系统平衡,则左、右两侧水银柱竖直部分应等高.
所以右边水银柱总长为
14 cm-(2 cm+8 cm)+2 cm=6 cm.
(2)以封闭气体为研究对象,设U管截面积为S
升温前,p1=78 cmHg V1=8S T0=273 K
升温后,p2=80 cmHg V2=12S T2=?
由理想气体状态方程,![]()
代入已知数据得,T2=420 K.
即当空气柱温度升高到420 K时,左边的水银恰好全部进入竖直管AB内.
(3)温度从420 K升高到490 K的过程中,为等压变化右边水银面保待不变,其高度为4 cm.
由盖·吕萨克定律:![]()
即![]()
∴l3=![]() l2
l2
代入已知数据得 l3=14 cm
所以左边的水银柱上表面高度为:14 cm-12 cm+4 cm=6 cm

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目