Question

【题目】如图所示，水平面上静止放置一个透明实心玻璃球，O点是球心，A是最高点，B是最低点。两条跟水平面夹角为45°的平行光线斜照在球面上，其中一条向着球心O，其延长线交地面于D点（图中未画出），另一条过最高点A。已知该玻璃的折射率为，。求：

（1）过A点的光线折射进入玻璃球时的折射角；

（2）过A点的光线从玻璃球射出后，跟水平面的交点是在D点的左侧、右侧、还是在D点？试证明你的猜想。

Answer 1

【答案】(1)；(2)见解析。

【解析】

(1) 由题意知，在A点入射角i=45°。设折射角为r，由折射定律得

解得

(2) 设E点为折射光线的出射点，由几何关系得

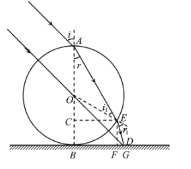
过E点做水平面的垂线，垂足为F；过E点做水平线，与AB的交点为C，由几何关系得

设光线在E点的入射角为i1，折射角为r1，由几何关系得

解得

设从玻璃球折射出的光线与水平面的交点为G，由几何关系得

解得

BG=R

经过圆心O的光线沿直线传播，由几何关系得可知

可知

BG=BD

所以，过A点的光线从玻璃球射出后，跟水平面的交点在D点。