题目内容
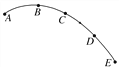
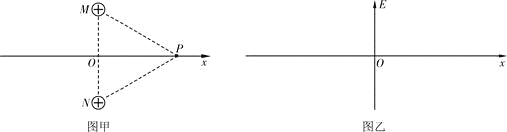
【题目】(1)如图甲所示,M、N是真空中两个电荷量均为+Q的固定点电荷,M、N间的距离为a;沿MN连线的中垂线建立坐标轴,P是x轴上的点,![]() °。已知静电力常量为k。
°。已知静电力常量为k。
a.求P点场强的大小和方向;
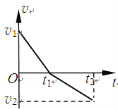
b.在图乙中定性画出场强E随x变化的图像(取向右为场强E的正方向)。
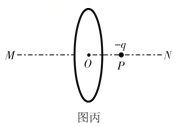
(2)如图丙所示,一个半径为R、电荷量为+Q的均匀带电圆环固定在真空中,环心为O,MN是其中轴线。现让一电荷量为q、质量为m的带电粒子从MN上的P点由静止释放,P、O间的距离为d。不计粒子重力。试证明:当d<< R时,带电粒子做简谐运动。
【答案】(1)a、![]() ,方向沿x轴正方向
,方向沿x轴正方向
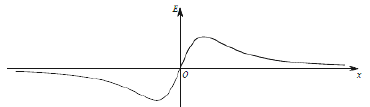
b、
(2)
【解析】试题分析:⑴a,如下图所示,M、N点的两个电荷在P点产生的场强分别为E1、E2

由电场的叠加原理和对称性可知,P点合场强的大小为![]() ,方向沿x轴正方向。
,方向沿x轴正方向。
B、O点场强为零,无穷远处场强为零,中间有一最大值。如下图所示

⑵如图所示,
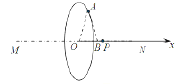
沿圆环的轴线建立坐标轴,O是原点。把圆环分成若干等份,每一份都很小,可视为点电荷。设每一份的电荷量为![]() Q,
Q,![]() ,当q运动到任意位置(x,0)时,圆环上任一小段A有沿x轴方向的场强,设∠APO=θ,则:
,当q运动到任意位置(x,0)时,圆环上任一小段A有沿x轴方向的场强,设∠APO=θ,则:
Q点所受合力![]()
由于x<d<<R,则![]()
即带电粒子q所受合外力与位移x成正比,总指向平衡位置,因此该离子做简谐运动。

练习册系列答案
相关题目