题目内容
9. 如图是遥控赛车比赛的过程展示图,赛车通电后以额定功率P=2W工作,从起点A由静止启动,沿水平直线轨道运动l后,由B点进入半径为R的光滑竖直圆轨道,轨道半径R=0.4m,入口的平直轨道AB和出口的平直轨道BC均是粗糙的,赛车质量m=0.1kg,与水平轨道之间的动摩擦因数均为μ=0.5,AB的长度l=10m,赛车在AB段中的某点就已经关闭电动机,取g=10m/s2,试问:
如图是遥控赛车比赛的过程展示图,赛车通电后以额定功率P=2W工作,从起点A由静止启动,沿水平直线轨道运动l后,由B点进入半径为R的光滑竖直圆轨道,轨道半径R=0.4m,入口的平直轨道AB和出口的平直轨道BC均是粗糙的,赛车质量m=0.1kg,与水平轨道之间的动摩擦因数均为μ=0.5,AB的长度l=10m,赛车在AB段中的某点就已经关闭电动机,取g=10m/s2,试问:(1)要使赛车恰好通过圆轨的最高点,小车在B点的速度为多少?
(2)满足(1)条件下,小车能沿着出口平直轨道BC滑行多远的距离?
(3)要使小车不脱离轨道,电动机工作多长时间?
分析 (1)小球恰好通过最高点求的最高点的速度,根据动能定理求的B点的速度;
(2)从B点到静止根据动能定理求的位移
(3)从A到B根据动能定理求得时间
解答 解:(1)下车恰好能通过最高点,故在最高点由牛顿第二定律可得$mg=\frac{m{v}^{2}}{R}$
从最高点到B点根据动能定理可得$mg•2R=\frac{1}{2}{mv}_{B}^{2}-\frac{1}{2}m{v}^{2}$
联立解得${v}_{B}=2\sqrt{5}m/s$
(2)由动能定理可的
$-μmgx=0-\frac{1}{2}{mv}_{B}^{2}$
解得x=2m
(3)从A到B根据动能定理可得$Pt-μmgl=\frac{1}{2}{mv}_{B}^{2}-0$
解得t=0.25s
答:(1)要使赛车恰好通过圆轨的最高点,小车在B点的速度为2$\sqrt{5}$m/s
(2)满足(1)条件下,小车能沿着出口平直轨道BC滑行2m
(3)要使小车不脱离轨道,电动机工作0.25s
点评 本题是力学综合题中多过程问题,关键要将物体的运动分为三个过程,分析清楚各个过程的运动特点和受力特点,然后根据动能定理、列式求解

练习册系列答案
相关题目
19.容器内盛有部分水,现将容器竖直向上抛出(设容器在上抛过程中不发生翻转),那么下列说法中正确的是( )
| A. | 上升过程中水对容器底面的压力逐渐增大 | |
| B. | 下降过程中水对容器底面的压力逐渐减小 | |
| C. | 在最高点水对容器底面的压力大小等于水的重力大小 | |
| D. | 整个过程中对容器底面都没有压力 |
20. 图是某一电场中的一条直线电场线,A、B是这条电场线上的两点,下列说法中正确的是( )
图是某一电场中的一条直线电场线,A、B是这条电场线上的两点,下列说法中正确的是( )
 图是某一电场中的一条直线电场线,A、B是这条电场线上的两点,下列说法中正确的是( )
图是某一电场中的一条直线电场线,A、B是这条电场线上的两点,下列说法中正确的是( )| A. | A点的电势能比B点的大 | |
| B. | A点的场强比B点的大 | |
| C. | 取B点的电势能为零时,负电荷在A点具有的电势能一定为负 | |
| D. | 取B点的电势能为零时,正电荷在A点具有的电势能一定为负 |
17.如图所示,两光滑小球均处于静止状态,关于它们受到的弹力情况的说法正确的是( )


| A. | 甲球受到两个弹力作用 | |
| B. | 乙球受到一个弹力作用 | |
| C. | 甲球受到的支持力垂直水平面向上 | |
| D. | 乙球受到绳子的拉力沿绳子方向向右 |
4. 用如图所示的电路测量一节蓄电池的电动势和内阻,蓄电池的内阻非常小,为防止调节滑动变阻器电阻过小时由于电流过大而损坏器材,电路中用了一个保护电阻R0,除蓄电池、开关、导线外,可供选择使用的实验器材还有:
用如图所示的电路测量一节蓄电池的电动势和内阻,蓄电池的内阻非常小,为防止调节滑动变阻器电阻过小时由于电流过大而损坏器材,电路中用了一个保护电阻R0,除蓄电池、开关、导线外,可供选择使用的实验器材还有:
(A)电流表(量程0.6A、3A)
(B)电压表(量程3V、15V)
(C)定值电阻(阻值1Ω、额定功率5W)
(F)定值电阻(阻值10Ω,额定功率10W)
(1)电流表和电压表各选哪个量程?选用哪个定值电阻做R0?
(2)某同学按图示进行实验,他调整滑动变阻器共得到5组数据.
请做出蓄电池路端电压U随电流I变化的U-I图象,根据图象得出蓄电池的电动势E=2.02,内阻r=0.08.
 用如图所示的电路测量一节蓄电池的电动势和内阻,蓄电池的内阻非常小,为防止调节滑动变阻器电阻过小时由于电流过大而损坏器材,电路中用了一个保护电阻R0,除蓄电池、开关、导线外,可供选择使用的实验器材还有:
用如图所示的电路测量一节蓄电池的电动势和内阻,蓄电池的内阻非常小,为防止调节滑动变阻器电阻过小时由于电流过大而损坏器材,电路中用了一个保护电阻R0,除蓄电池、开关、导线外,可供选择使用的实验器材还有:(A)电流表(量程0.6A、3A)
(B)电压表(量程3V、15V)
(C)定值电阻(阻值1Ω、额定功率5W)
(F)定值电阻(阻值10Ω,额定功率10W)
(1)电流表和电压表各选哪个量程?选用哪个定值电阻做R0?
(2)某同学按图示进行实验,他调整滑动变阻器共得到5组数据.
| 1 | 2 | 3 | 4 | 5 | |
| U(V) | 1.88 | 1.92 | 1.93 | 1.98 | 1.99 |
| I(A) | 1.72 | 1.35 | 0.98 | 0.63 | 0.34 |
10. 一列长100m的火车匀加速通过长1000m的桥梁,列车刚上桥的速度为10m/s,完全离开桥梁的速度为12m/s.则下列说法正确的是( )
一列长100m的火车匀加速通过长1000m的桥梁,列车刚上桥的速度为10m/s,完全离开桥梁的速度为12m/s.则下列说法正确的是( )
 一列长100m的火车匀加速通过长1000m的桥梁,列车刚上桥的速度为10m/s,完全离开桥梁的速度为12m/s.则下列说法正确的是( )
一列长100m的火车匀加速通过长1000m的桥梁,列车刚上桥的速度为10m/s,完全离开桥梁的速度为12m/s.则下列说法正确的是( )| A. | 火车完全通过此桥梁的平均速度为11m/s | |
| B. | 火车完全通过此桥梁的时间为100s | |
| C. | 火车完全通过此桥梁的加速度为0.02m/s2 | |
| D. | 火车在桥梁上运动的时间为81.80s |
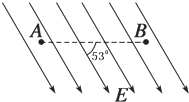 如图所示,在匀强电场中,有A、B两点,它们之间的距离为10cm,两点的连线与场强方向成53°角.将一个电荷量为1×10-6 C的电荷由A点移到B点,电场力做功为8×10-5 J.求:
如图所示,在匀强电场中,有A、B两点,它们之间的距离为10cm,两点的连线与场强方向成53°角.将一个电荷量为1×10-6 C的电荷由A点移到B点,电场力做功为8×10-5 J.求: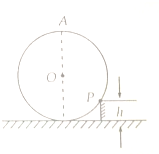 一个质量为m=50kg的均匀圆柱体,放在台阶的旁边,台阶的高度h是柱体半径的一半,如图所示(图示为其横截面),柱体与台阶的接触处(图中P点所示)是粗糙的.现要在圆柱体的最上方A处施加最小的拉力,使柱体刚能开始以P为轴向台阶上滚,求所施加的力F1的大小及P点对圆柱体的作用力F2的大小(g=10N/kg).
一个质量为m=50kg的均匀圆柱体,放在台阶的旁边,台阶的高度h是柱体半径的一半,如图所示(图示为其横截面),柱体与台阶的接触处(图中P点所示)是粗糙的.现要在圆柱体的最上方A处施加最小的拉力,使柱体刚能开始以P为轴向台阶上滚,求所施加的力F1的大小及P点对圆柱体的作用力F2的大小(g=10N/kg).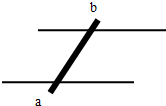 两条相距为1m的水平金属导轨上放置一根导电棒ab,处于竖直方向的匀强磁场中,如图所示,导电棒的质量是1.2kg,当棒中通入2A的电流时(电流方向是从a到b),它可在导轨上向右匀速滑动,如电流增大到4A时,棒可获得0.5m/s2的加速度.求:
两条相距为1m的水平金属导轨上放置一根导电棒ab,处于竖直方向的匀强磁场中,如图所示,导电棒的质量是1.2kg,当棒中通入2A的电流时(电流方向是从a到b),它可在导轨上向右匀速滑动,如电流增大到4A时,棒可获得0.5m/s2的加速度.求: