题目内容
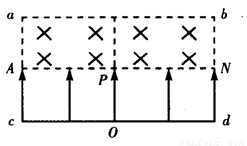
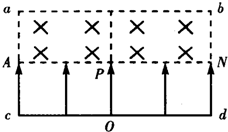 如图所示,一束质量为m、电荷量为q的带正电粒子从O点由静止开始经过匀强电场加速后,均从边界AN的中点P垂直于AN和磁场方向射入磁感应强度为B=
如图所示,一束质量为m、电荷量为q的带正电粒子从O点由静止开始经过匀强电场加速后,均从边界AN的中点P垂直于AN和磁场方向射入磁感应强度为B=| 3 |
| R |
|
| 1 |
| 2 |
| 1 |
| 2 |
(1)若加速电场加速电压为9U,求粒子在电磁场中运动的总时间;
(2)若加速电场加速电压为U,求粒子在电磁场中运动的总时间.
分析:(1)根据动能定理求出粒子加速获得的速度.由运动学公式求出加速的时间.粒子进入磁场后做匀速圆周运动,由洛伦兹力提供向心力,根据牛顿第二定律和向心力公式求出轨迹半径,画出轨迹,由几何知识确定轨迹对应的圆心角,即可求得磁场中运动时间,从而得到总时间.
(2)若加速电场加速电压为U时,运用同样的思路求出粒子电场中的运动时间和磁场中的轨迹半径,画出运动轨迹,根据运动情况,求解磁场中的时间.即可得到总时间.
(2)若加速电场加速电压为U时,运用同样的思路求出粒子电场中的运动时间和磁场中的轨迹半径,画出运动轨迹,根据运动情况,求解磁场中的时间.即可得到总时间.
解答: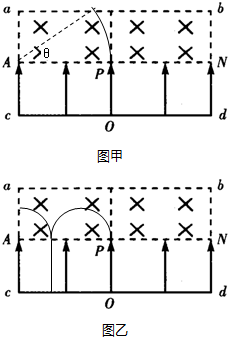 解:(1)若加速电场加速电压为9U,由动能定理得:
解:(1)若加速电场加速电压为9U,由动能定理得:
q?9U=
mv2,得 v=
在磁场中,粒子做匀速圆周运动,由洛伦兹力提供向心力,由牛顿第二定律得:
qvB=m
又 B=
解得,r=R
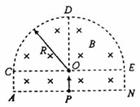
画出粒子的运动轨迹如图甲所示,由几何关系可得,轨迹对应的圆心角为 θ=30°;
带电粒子在磁场中运动的时间为 tB=
T=
×
=
粒子在电场中做匀加速直线运动,则有:d=
R=
tE
解得,tE=R
故粒子在电磁场中运动的总时间为 t总=tE+tB=(
+
)R
(2)若加速电场加速电压为U,由动能定理得:
qU=
mv′2,得:v′=
在磁场中,根据牛顿第二定律得:
qv′B=m
解得,r′=
分析可知粒子在磁场中运动的轨迹为一个半圆和四分之一圆周如图乙所示,
带电粒子在磁场中运动的周期为 TB=
,
则粒子在磁场中运动的时间为 tB′=
TB
分析可知粒子在电场中先加速后减速再加速,由运动学公式可得:tE′=
=R
则粒子在电场中运动的时间为3tB′=3R
故粒子在电磁场中运动的总时间为t′=tB′+3tB′=(2π+3)R
答:(1)若加速电场加速电压为9U,粒子在电磁场中运动的总时间为(
+
)R
;
(2)若加速电场加速电压为U,粒子在电磁场中运动的总时间(2π+3)R
.
 解:(1)若加速电场加速电压为9U,由动能定理得:
解:(1)若加速电场加速电压为9U,由动能定理得:q?9U=
| 1 |
| 2 |
|
在磁场中,粒子做匀速圆周运动,由洛伦兹力提供向心力,由牛顿第二定律得:
qvB=m
| v2 |
| r |
又 B=
| 3 |
| R |
|
解得,r=R
画出粒子的运动轨迹如图甲所示,由几何关系可得,轨迹对应的圆心角为 θ=30°;
带电粒子在磁场中运动的时间为 tB=
| θ |
| 360° |
| 30° |
| 360° |
| 2πm |
| qB |
| πm |
| 6qB |
粒子在电场中做匀加速直线运动,则有:d=
| 1 |
| 2 |
| v |
| 2 |
解得,tE=R
|
故粒子在电磁场中运动的总时间为 t总=tE+tB=(
| π |
| 18 |
| 1 |
| 3 |
|
(2)若加速电场加速电压为U,由动能定理得:
qU=
| 1 |
| 2 |
|
在磁场中,根据牛顿第二定律得:
qv′B=m
| v′2 |
| r′ |
解得,r′=
| R |
| 3 |
分析可知粒子在磁场中运动的轨迹为一个半圆和四分之一圆周如图乙所示,
带电粒子在磁场中运动的周期为 TB=
| 2πm |
| qB |
则粒子在磁场中运动的时间为 tB′=
| 3 |
| 4 |
分析可知粒子在电场中先加速后减速再加速,由运动学公式可得:tE′=
| ||
|
|
则粒子在电场中运动的时间为3tB′=3R
|
故粒子在电磁场中运动的总时间为t′=tB′+3tB′=(2π+3)R
|
答:(1)若加速电场加速电压为9U,粒子在电磁场中运动的总时间为(
| π |
| 18 |
| 1 |
| 3 |
|
(2)若加速电场加速电压为U,粒子在电磁场中运动的总时间(2π+3)R
|
点评:本题画出带电粒子的运动轨迹,由几何知识求出轨迹对应的圆心角是解决本题的关键,根据时间与周期的关系求解磁场中运动时间是常规思路.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
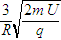 的匀强磁场中。已知匀强电场的宽度为d=
的匀强磁场中。已知匀强电场的宽度为d=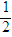 R,匀强磁场由一个长为2R、宽为
R,匀强磁场由一个长为2R、宽为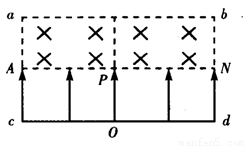
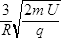 的匀强磁场中。已知匀强电场的宽度为d=
的匀强磁场中。已知匀强电场的宽度为d=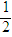 R,匀强磁场由一个长为2R、宽为
R,匀强磁场由一个长为2R、宽为