Question

如图16所示为某种弹射装置的示意图，光滑的水平导轨MN右端N处与水平传送带理想连接，传送带长度 L = 4.0 m，皮带轮沿顺时针方向转动，带动皮带以恒定速率v = 3.0 m/s 匀速传动．三个质量均为m = 1.0 kg 的滑块A、B、C置于水平导轨上，开始时滑块B、C之间用细绳相连，其间有一压缩的轻弹簧，处于静止状态．滑块A以初速度v₀ = 2.0 m/s 沿B、C连线方向向B运动，A与B碰撞后粘合在一起，碰撞时间极短．连接B、C的细绳受扰动而突然断开，弹簧伸展，从而使C与A、B分离．滑块C脱离弹簧后以速度v_C = 2.0 m／s 滑上传送带，并从右端滑出落至地面上的P点．

已知滑块C与传送带之间的动摩擦因数μ = 0.20，重力加速度g取10 m／s²．求：

（1）滑块C从传送带右端滑出时的速度大小； 

（2）滑块B、C用细绳相连时弹簧的弹性势能E_p；

（3）若每次实验开始时弹簧的压缩情况相同，要使滑块C总能落至P点，则滑块A与滑块B碰撞前速度的最大值V_m是多少?

 

Answer 1

【答案】

（1）滑块C滑上传送带后做匀加速运动，设滑块C从滑上传送带到速度达到传送带的速度v所用的时间为t，加速度大小为a，在时间t内滑块C的位移为x．

根据牛顿第二定律和运动学公式 μmg=ma，   

v=v_C+at，  

．

解得  x=1.25m＜L…………………………………………………………………２分

即滑块C在传送带上先加速，达到传送带的速度v后随传送带匀速运动，并从右端滑出，则滑块C从传送带右端滑出时的速度为v=3.0m/s………………………………２分  

（2）设A、B碰撞后的速度为v₁，A、B与C分离时的速度为v₂，由动量守恒定律

mv₀=2mv­₁ ……………………………………………………………１分

      　　　　2 mv₁=2mv­₂+mv_C ……………………………………………………１分

由能量守恒得 ……………………………１分

解得　　　　E_P=1.0J ……………………………………………………………１分

   （3）在题设条件下，若滑块A在碰撞前速度有最大值，则碰撞后滑块C的速度有最大值，它减速运动到传送带右端时，速度应当恰好等于传递带的速度v．  

设A与B碰撞后的速度为，分离后A与B的速度为，滑块C的速度为，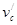

由动量守恒定律   

mv_m=2mv₁′    

2mv₁′=mv_C′+2mv₂′　　……………………………………………１分

由能量守恒得　　………………………１分

由运动学公式 　　………………………………………………１分

解得　　　　v_m=7.1m/s　　………………………………………………………１分

【解析】略