Question

【题目】如图所示，在水平方向的匀强电场中有一表面光滑、与水平面成45°角的绝缘直杆AC，其下端（C端）距地面高度h＝0．8 m．有一质量为500 g的带电小环套在直杆上，正以某一速度沿杆匀速下滑．小球离杆后正好通过C端的正下方P点处．（g取10 m/s2）求：

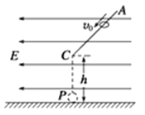
（1）小环离开直杆后运动的加速度大小和方向；

（2）小环从C运动到P过程中的动能增量；

（3）小环在直杆上匀速运动时速度的大小v0．

Answer 1

【答案】（1）10m/s2，方向垂直于杆向下（或与水平方向成45°角斜向下）（2）4J（3）2m/s

【解析】

试题分析：（1）对带电小环受力分析

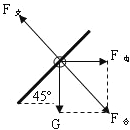
因带电小环匀速下滑，加之电场强度水平向左，所以小环带负电．

由几何关系可知，小环所受电场力与重力大小相等．则小环离开直杆后所受的合外力大小为：F合=mg

由牛顿第二定律可得：a＝g＝10m/s2，方向垂直于杆向下（或与水平方向成45°角斜向下）．

（2）设小环从C运动到P过程中动能的增量为△Ek．由动能定理有：WG+WE=△Ek

则电场力做功为零WE=0

所以△Ek=WG=mgh=4J

（3）小环离开杆做类平抛运动．如图所示建立坐标x、y轴

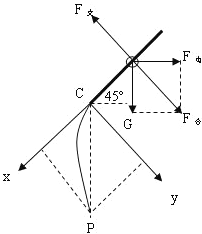
垂直于杆方向做匀加速运动：

平行于杆方向做匀速运动：x＝v0t＝

解得：υ0=2m/s