题目内容
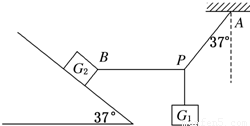
 所受重力G1=8N的砝码悬挂在绳PA和PB的结点上.PA偏离竖直方向37°角,PB在水平方向,且连在所受重力为G2=100N的木块上,木块静止于倾角为37°的斜面上,如图所示,试求:(
所受重力G1=8N的砝码悬挂在绳PA和PB的结点上.PA偏离竖直方向37°角,PB在水平方向,且连在所受重力为G2=100N的木块上,木块静止于倾角为37°的斜面上,如图所示,试求:(sin53°=0.8 cos53°=0.6,重力加速度g取10m/s2)
(1)木块与斜面间的摩擦力大小;
(2)木块所受斜面的弹力大小.
分析:(1)先对P点受力分析,受到三根绳子的三个拉力,然后根据共点力平衡条件,运用正交分解法求解出各个力;再对斜面上的物体受力分析,受到重力、拉力、支持力和摩擦力,再次根据共点力平衡条件列方程求解即可;
(2)与第一问的解法相同.
(2)与第一问的解法相同.
解答: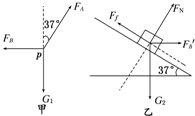 解:(1)如图甲所示分析P点受力,由平衡条件可得:
解:(1)如图甲所示分析P点受力,由平衡条件可得:
FA cos37°=G1
FA sin37°=FB
可解得:FB=6 N
再分析G2的受力情况,如图乙所示
由物体的平衡条件可得:
Ff=G2 sin37°+FB′cos37°
FN+FB′sin37°=G2 cos37°
FB′=FB
可求得:Ff=64.8 N
FN=76.4 N
即木块与斜面间的摩擦力大小为64.8N;
(2)由第一问的解答可以得到:FN=76.4 N
即木块所受斜面的弹力大小为76.4 N.
 解:(1)如图甲所示分析P点受力,由平衡条件可得:
解:(1)如图甲所示分析P点受力,由平衡条件可得:FA cos37°=G1
FA sin37°=FB
可解得:FB=6 N
再分析G2的受力情况,如图乙所示
由物体的平衡条件可得:
Ff=G2 sin37°+FB′cos37°
FN+FB′sin37°=G2 cos37°
FB′=FB
可求得:Ff=64.8 N
FN=76.4 N
即木块与斜面间的摩擦力大小为64.8N;
(2)由第一问的解答可以得到:FN=76.4 N
即木块所受斜面的弹力大小为76.4 N.
点评:本题关键先后对结点P和斜面上物体受力分析,然后根据共点力平衡条件列方程求解出各个力.

练习册系列答案
相关题目
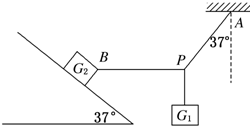 所受重力G1=8N的砝码悬挂在绳PA和PB的结点上.PA偏离竖直方向37°角,PB在水平方向,且连在所受重力为G2=100N的木块上,木块静止于倾角为37°的斜面上,如图所示,试求:
所受重力G1=8N的砝码悬挂在绳PA和PB的结点上.PA偏离竖直方向37°角,PB在水平方向,且连在所受重力为G2=100N的木块上,木块静止于倾角为37°的斜面上,如图所示,试求: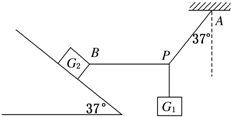 所受重力G1=8N的砝码悬挂在绳PA和PB的结点上,PA偏离竖直方向37°角,PB在水平方向,且连在所受重力为G2=100N的木块上,木块静止于倾角为37°的斜面上,如图所示,试求:
所受重力G1=8N的砝码悬挂在绳PA和PB的结点上,PA偏离竖直方向37°角,PB在水平方向,且连在所受重力为G2=100N的木块上,木块静止于倾角为37°的斜面上,如图所示,试求: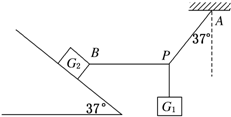
 所受重力G1=8N的砝码悬挂在绳PA和PB的结点上.PA偏离竖直方向37°角,PB在水平方向,且连在所受重力为G2=100N的木块上,木块静止于倾角为37°的斜面上,如图所示,试求:
所受重力G1=8N的砝码悬挂在绳PA和PB的结点上.PA偏离竖直方向37°角,PB在水平方向,且连在所受重力为G2=100N的木块上,木块静止于倾角为37°的斜面上,如图所示,试求: