题目内容
 如图所示,一根劲度系数为k的弹簧,上端系在天花板上,下端系一质量为mA的物体A,A通过一段细线吊一质量为mB的物体B,整个装置静止.若用剪刀将细线剪断,当A上升到弹力为零处时速度为v.则:剪断绳前弹簧的伸长量为
如图所示,一根劲度系数为k的弹簧,上端系在天花板上,下端系一质量为mA的物体A,A通过一段细线吊一质量为mB的物体B,整个装置静止.若用剪刀将细线剪断,当A上升到弹力为零处时速度为v.则:剪断绳前弹簧的伸长量为| (mA+mB)g |
| k |
| (mA+mB)g |
| k |
| 1 |
| 2 |
| mA(mA+mB)g2 |
| k |
| 1 |
| 2 |
| mA(mA+mB)g2 |
| k |
分析:剪断绳前,对A和B整体受力分析,整体受重力和弹簧的拉力.根据平衡条件求解弹簧的伸长量.
研究剪断绳到A物体上升到弹力为零的过程中,根据动能定理列出等式求解弹力对A物体做的功.
研究剪断绳到A物体上升到弹力为零的过程中,根据动能定理列出等式求解弹力对A物体做的功.
解答:解:(1)剪断绳前,对A和B整体受力分析,整体受重力和弹簧的拉力.
根据平衡条件得:(mA+mB)g=F
根据胡克定律得:F=kx
解得:x=
(2)研究剪断绳到A物体上升到弹力为零的过程中,根据动能定理得:
w弹+(-mAgx)=
mAv2-0
w弹=
mAv2+mAg
=
mAv2+
故答案为:
,
mAv2+
.
根据平衡条件得:(mA+mB)g=F
根据胡克定律得:F=kx
解得:x=
| (mA+mB)g |
| k |
(2)研究剪断绳到A物体上升到弹力为零的过程中,根据动能定理得:
w弹+(-mAgx)=
| 1 |
| 2 |
w弹=
| 1 |
| 2 |
| (mA+mB)g |
| k |
| 1 |
| 2 |
| mA(mA+mB)g2 |
| k |
故答案为:
| (mA+mB)g |
| k |
| 1 |
| 2 |
| mA(mA+mB)g2 |
| k |
点评:解答本题时要注意两点:一是正确选取研究对象,并能进行正确的受力分析;二是能选择运用动能定理求解变力功.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
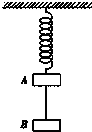 如图所示,一根劲度系数为k的弹簧,上端系在天花板上,下端系一质量为mA的物体A,A通过一段细线吊一质量为mB的物体B整个装置静止.试求:
如图所示,一根劲度系数为k的弹簧,上端系在天花板上,下端系一质量为mA的物体A,A通过一段细线吊一质量为mB的物体B整个装置静止.试求:
 点的最远距离为多少?(假设最大静摩擦力等于滑动摩擦力)
点的最远距离为多少?(假设最大静摩擦力等于滑动摩擦力)