题目内容
15. 如图所示,一个质量为M的人,站在台秤上,手拿一个质量为m,悬线长为R的小球,在竖直平面内做圆周运动,且摆球正好通过圆轨道最高点,在运动中台秤示数F的可能值为( )
如图所示,一个质量为M的人,站在台秤上,手拿一个质量为m,悬线长为R的小球,在竖直平面内做圆周运动,且摆球正好通过圆轨道最高点,在运动中台秤示数F的可能值为( )| A. | F=(M+7m)g | B. | F=(M+5m)g | C. | F=(M-m)g | D. | F=(M-0.5m)g |
分析 根据牛顿第二定律分析摆球的受力情况进而结合向心力和牛顿第三定律得到台秤示数.
解答 解:摆球正好通过圆轨道最高点,则最高点有:
$mg=\frac{m{v}_{1}^{2}}{R}$
最高点到最低点的过程中有:
$\frac{1}{2}m{v}_{1}^{2}+mg•2R=\frac{1}{2}m{v}_{2}^{2}$
最低点有:${F}_{m}-mg=\frac{m{v}_{2}^{2}}{R}$
得:Fm=6mg
所以台秤的最大示数为:Fmax=Mg+6mg
当小球经过如题图所示的状态时,设绳子与竖直方向之间的夹角是θ,其速度为v则有:
$\frac{1}{2}$mv2=$\frac{1}{2}$mv02+mgR(1-cosθ)
根据牛顿第二定律有:
T+mgcosθ=m$\frac{{v}^{2}}{R}$
解得:T=3mg(1-cosθ)
其分力Ty=Tcosθ=3mgcosθ-3mgcos2θ
当cosθ=$\frac{1}{2}$,即θ=60°时,Ty最大,此时Tymax=0.75mg
故台秤的最小示数Fmin=(M-0.75m)g
可知台秤的示数范围:(M-0.75m)g≤F≤Mg+6mg
故选:BD
点评 本题综合性较强,由物理知识表示出T于θ的几何关系,然后由数学知识求极值.

练习册系列答案
相关题目
6.下图中哪一个图是正确的( )
| A. |  | B. |  | C. | 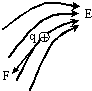 | D. | 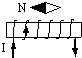 |
3.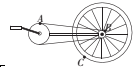 如图所示,自行车的大齿轮、小齿轮、后轮的半径不一样,它们的边缘有三个点A、B、C,匀速转动大齿轮,带动小齿轮和后轮,则下列说法正确的是( )
如图所示,自行车的大齿轮、小齿轮、后轮的半径不一样,它们的边缘有三个点A、B、C,匀速转动大齿轮,带动小齿轮和后轮,则下列说法正确的是( )
 如图所示,自行车的大齿轮、小齿轮、后轮的半径不一样,它们的边缘有三个点A、B、C,匀速转动大齿轮,带动小齿轮和后轮,则下列说法正确的是( )
如图所示,自行车的大齿轮、小齿轮、后轮的半径不一样,它们的边缘有三个点A、B、C,匀速转动大齿轮,带动小齿轮和后轮,则下列说法正确的是( )| A. | A、B两点的线速度大小相等 | B. | B、C两点的线速度大小相等 | ||
| C. | A、C两点的转速相同 | D. | B、C两点的周期相同 |
10.如图所示是一个由电池、电阻R与平行板电容器组成的电路,在减小电容器两板间距离的过程中( )
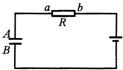

| A. | 电阻R中没有电流 | B. | 电容器的电容变大 | ||
| C. | 电阻R中有从a流向b的电流 | D. | 电阻R中有从b流向a的电流 |
20. 如图所示,A、B两物体叠放在水平面上,水平力F作用在A上,使两者一起向右做匀速直线运动,下列判断错误的是( )
如图所示,A、B两物体叠放在水平面上,水平力F作用在A上,使两者一起向右做匀速直线运动,下列判断错误的是( )
 如图所示,A、B两物体叠放在水平面上,水平力F作用在A上,使两者一起向右做匀速直线运动,下列判断错误的是( )
如图所示,A、B两物体叠放在水平面上,水平力F作用在A上,使两者一起向右做匀速直线运动,下列判断错误的是( )| A. | B与地面间无摩擦力 | |
| B. | A对B的静摩擦力大小为F,方向向右 | |
| C. | B对地面的动摩擦力的大小为F,方向向右 | |
| D. | B受到了向右的静摩擦力和向左的滑动摩擦力 |
7. 设竖直向上为y轴正方向,如图曲线为一质点沿y轴运动的位置-时间(y-t)图象,已知图线为一条抛物线,则由图可知( )
设竖直向上为y轴正方向,如图曲线为一质点沿y轴运动的位置-时间(y-t)图象,已知图线为一条抛物线,则由图可知( )
 设竖直向上为y轴正方向,如图曲线为一质点沿y轴运动的位置-时间(y-t)图象,已知图线为一条抛物线,则由图可知( )
设竖直向上为y轴正方向,如图曲线为一质点沿y轴运动的位置-时间(y-t)图象,已知图线为一条抛物线,则由图可知( )| A. | t=0时刻质点速度为0 | |
| B. | 0~t1时间内质点向y轴负方向运动 | |
| C. | 0~t2时间内质点的速度一直减小 | |
| D. | t1~t3时间内质点相对坐标原点O的位移先为正后为负 |
5.在《用打点计时器测速度》实验中,
(1)需要的器材有:打点计时器、(长木板、)复写纸片、4-6V低压交变电源、纸带、刻度尺
(2)下列说法正确的是B
A.拖动纸带的同时,闭合电源开关
B.先闭合电源开关,让打点计时器正常工作时,拖动纸带
C.纸带上的打点密集说明,纸带运动速度较大
D.利用打出的纸带可以准确的求出打下某些点时纸带运动的瞬时速度
(3)某同学拖动纸带运动,打点计时器在纸带上打出一系列点,处理时每隔1个点取一个记数点,标上字母A、B、C、D、E、F.
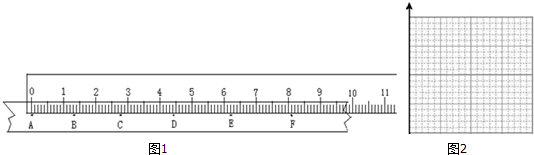
如图1所示,某同学用mm刻度尺进行测量,请帮忙读出B、C、D、F在刻度尺上的位置,填到表中:
由读出数据可计算出打下AF段纸带时小车的平均速度为4.05m/s.
(4)若认为一段时间中间时刻的瞬时速度就是这段时间内的平均速度,则打点计时器打下C点时小车的速度VC=0.388m/s,小车从C点运动D点过程中的加速度a=1.00m/s2.
(5)在图2所给坐标纸上建好坐标,作出纸带运动的打下B至E点的速度-时间图象(即v-t图象)(从打下A点开始计时).
(1)需要的器材有:打点计时器、(长木板、)复写纸片、4-6V低压交变电源、纸带、刻度尺
(2)下列说法正确的是B
A.拖动纸带的同时,闭合电源开关
B.先闭合电源开关,让打点计时器正常工作时,拖动纸带
C.纸带上的打点密集说明,纸带运动速度较大
D.利用打出的纸带可以准确的求出打下某些点时纸带运动的瞬时速度
(3)某同学拖动纸带运动,打点计时器在纸带上打出一系列点,处理时每隔1个点取一个记数点,标上字母A、B、C、D、E、F.

如图1所示,某同学用mm刻度尺进行测量,请帮忙读出B、C、D、F在刻度尺上的位置,填到表中:
| 计数点 | B | C | D | E | F |
| 位置(cm) | 4.44 | 6.22 | 8.12 |
(4)若认为一段时间中间时刻的瞬时速度就是这段时间内的平均速度,则打点计时器打下C点时小车的速度VC=0.388m/s,小车从C点运动D点过程中的加速度a=1.00m/s2.
(5)在图2所给坐标纸上建好坐标,作出纸带运动的打下B至E点的速度-时间图象(即v-t图象)(从打下A点开始计时).