题目内容
主截面是边长为d的正方形的棱柱,折射率为n,将其弯成半圆形(如图20-26所示).要使A端垂直入射的光线全部从B端射出,求所弯半圆形的最小内半径R的值.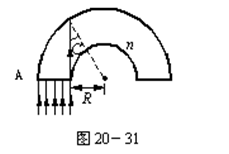

R=d/(n-1)。
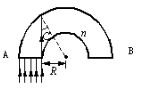
要使光线全部由B端射出,则要求射入棱柱的光线全部发生全反射,而不能发生折射。那么从A端入射的光线中,只要使最易发生折射的光线发生全反射,则可满足题目要求。最易发生折射的光线应为入射角最小的光线,由图可看出A端最内侧的光线其入射角最小,因此必须保证此光线能发生全反射,即此光线的入射角等于或大于临界角.由图中的几何关系可看出,此光线入射角的正弦值为:sinC=R/(R+d)(由折射定律可知sinC=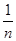 ),由此可解得半圆的最小内半径为R=d/(n-1)。
),由此可解得半圆的最小内半径为R=d/(n-1)。
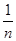 ),由此可解得半圆的最小内半径为R=d/(n-1)。
),由此可解得半圆的最小内半径为R=d/(n-1)。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
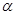 ,光在真空中的传播速度为c.求:该色光穿过玻璃砖所用的时间与入射角
,光在真空中的传播速度为c.求:该色光穿过玻璃砖所用的时间与入射角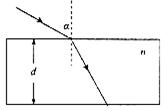
 ,它们的光路可能是下图5中的
,它们的光路可能是下图5中的

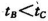 B.
B.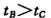
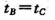 D.因入射角未知,无法比较tB、tC
D.因入射角未知,无法比较tB、tC