题目内容
 如图所示,两个质量都是M=0.4Kg的砂箱A、B并排放在光滑的水平面上,一颗质量为m=0.1Kg的子弹以v0=140m/s的水平速度射向A.射穿A后,进入B并同B一起运动,测得A、B落地点到桌边缘的水平距离之比为1:2.取g=10m/s2,求
如图所示,两个质量都是M=0.4Kg的砂箱A、B并排放在光滑的水平面上,一颗质量为m=0.1Kg的子弹以v0=140m/s的水平速度射向A.射穿A后,进入B并同B一起运动,测得A、B落地点到桌边缘的水平距离之比为1:2.取g=10m/s2,求(1)A、B做平抛运动的初速度各多大?
(2)子弹在砂箱A、B中穿行时分别产生多少热量?
分析:(1)子弹在与AB木块作用时,不受外力,动量守恒,根据动量守恒定律列出方程,AB两木块离开桌面后做平抛运动,根据平抛运动的规律得到两个初速度的关系,联立求解即可.
(2)根据能量的转化和守恒关系得子弹在穿过A和射进B时产生的热量.
(2)根据能量的转化和守恒关系得子弹在穿过A和射进B时产生的热量.
解答:解:(1)A、B平抛运动的高度相等,由h=
gt2知,平抛运动的时间相等.
由水平位移x=v0t知,A、B落地点到桌边缘的水平距离之比为1:2,则A、B平抛初速度之比为1:2.
设A做平抛运动的初速度为v,则B做平抛运动的初速度为2v.
对子弹及A、B由动量守恒定律列方程得:
mv0=Mv+(M+m)?2v
则得 v=
=
m/s=10m/s
故A、B平抛运动的初速度分别为10m/s和20m/s
(2)设子弹穿过A后子弹的速度为v′,则得
mv0=2Mv+mv′
代入解得 v′=60m/s
由能量守恒得子弹在砂箱A、B中穿行时分别产生热量
QA=
m
-
mv′2-
?2Mv2=760J;
QB=
mv′2+
Mv2-
(M+m)(2v)2=100J
答:
(1)A、B做平抛运动的初速度分别为10m/s,20m/s.
(2)子弹在砂箱A、B中穿行时分别产生760J,100J的热量.
| 1 |
| 2 |
由水平位移x=v0t知,A、B落地点到桌边缘的水平距离之比为1:2,则A、B平抛初速度之比为1:2.
设A做平抛运动的初速度为v,则B做平抛运动的初速度为2v.
对子弹及A、B由动量守恒定律列方程得:
mv0=Mv+(M+m)?2v
则得 v=
| mv0 |
| 3M+2m |
| 0.1×140 |
| 3×0.4+2×0.1 |
故A、B平抛运动的初速度分别为10m/s和20m/s
(2)设子弹穿过A后子弹的速度为v′,则得
mv0=2Mv+mv′
代入解得 v′=60m/s
由能量守恒得子弹在砂箱A、B中穿行时分别产生热量
QA=
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| 1 |
| 2 |
QB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
答:
(1)A、B做平抛运动的初速度分别为10m/s,20m/s.
(2)子弹在砂箱A、B中穿行时分别产生760J,100J的热量.
点评:本题主要考查了动量守恒定律、平抛运动的基本规律、能量的转化和守恒关系的直接应用,难度适中.

练习册系列答案
相关题目
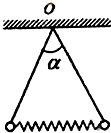 如图所示,两个质量都为m的完全相同的小球,分别用两根等长的细线悬挂在O点,两球之间夹着一根劲度系数为k的轻弹簧,静止时弹簧位于水平方向,两根细线的夹角为α,则以下说法正确的是( )
如图所示,两个质量都为m的完全相同的小球,分别用两根等长的细线悬挂在O点,两球之间夹着一根劲度系数为k的轻弹簧,静止时弹簧位于水平方向,两根细线的夹角为α,则以下说法正确的是( )A、弹簧的长度压缩了
| ||||
B、弹簧的长度压缩了
| ||||
C、弹簧受到的合力为2mgtan(
| ||||
| D、弹簧的弹力大小为2mgtanα |
 (2013?桂林一模)如图所示,两个质量都是m的小球A、B用轻杆连接后靠在墙上处于平衡状态,已知墙面光滑,水平地面粗糙,现将A球向上移动一小段距离,两球再次达到平衡,那么将移动后平衡状态和原来的平衡状态比较,地面对B球的支持力F1和摩擦力F2的大小变化情况是( )
(2013?桂林一模)如图所示,两个质量都是m的小球A、B用轻杆连接后靠在墙上处于平衡状态,已知墙面光滑,水平地面粗糙,现将A球向上移动一小段距离,两球再次达到平衡,那么将移动后平衡状态和原来的平衡状态比较,地面对B球的支持力F1和摩擦力F2的大小变化情况是( )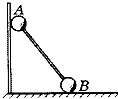 如图所示,两个质量都是m的小球A、B用轻杆连接后斜放在墙上处于平衡状态.已知墙面光滑,水平地面粗糙.现将A球向上移动一小段距离.两球再次达到平衡,那么将移动后的平衡状态和原来的平衡状态比较,地面对B球的支持力N和轻杆上的压力T的变化情况是( )
如图所示,两个质量都是m的小球A、B用轻杆连接后斜放在墙上处于平衡状态.已知墙面光滑,水平地面粗糙.现将A球向上移动一小段距离.两球再次达到平衡,那么将移动后的平衡状态和原来的平衡状态比较,地面对B球的支持力N和轻杆上的压力T的变化情况是( )