题目内容
(7分)如图所示,一水平传送装置由轮半径均为R= m的主动轮Q1和从动轮Q2及传送带等构成.两轮轴心相距lAB=8.0 m,轮与传送带不打滑.现用此装置运送一袋面粉,已知这袋面粉与传送带之间的动摩擦因数μ=0.4,这袋面粉中的面粉可不断地从袋中渗出.(g取10 m/s2)
m的主动轮Q1和从动轮Q2及传送带等构成.两轮轴心相距lAB=8.0 m,轮与传送带不打滑.现用此装置运送一袋面粉,已知这袋面粉与传送带之间的动摩擦因数μ=0.4,这袋面粉中的面粉可不断地从袋中渗出.(g取10 m/s2)

(1)当传送带以4.0 m/s的速度匀速运动时,将这袋面粉由左端Q2正上方的A点轻放在传送带上后,这袋面粉由A端运送到Q1正上方的B端所用的时间为多少?
(2)要想尽快将这袋面粉由A端送到B端(设初速度仍为零),主动轮Q1的转速至少应为多大?
(3)由于面粉的渗漏,在运送这袋面粉的过程中会在深色传送带上留下白色痕迹,这袋面粉在传送带上留下的痕迹最长能有多长(设袋的初速度仍为零)?此时主动轮的转速应满足何种条件?
(1)2.5 s(2)40 r/min(3)18.0 m n′≥390 r/min(或6.5 r/s)
【解析】设面粉袋的质量为m,其在与传送带产生相对滑动的过程中所受的摩擦力f=μmg
故而其加速度为:a=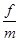 =μg=4.0 m/s2.
=μg=4.0 m/s2.
(1)若传送带的速度v带=4.0 m/s,则:
面粉袋加速运动的时间t1=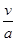 =1.0 s
=1.0 s
在t1时间内面粉袋的位移s1=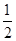 at
at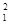 =2.0 m
=2.0 m
其后以v=4.0 m/s的速度做匀速运动
s2=lAB-s1=vt2 解得:t2=1.5 s
故这袋面粉运动的总时间为:t=t1+t2=2.5 s.
(2)要想时间最短,面粉袋应一直向B端做加速运动,由lAB=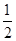 at′2可得:t′=2.0 s
at′2可得:t′=2.0 s
此时传送带的运转速度最小为:v′=at′=8.0 m/s
v=ωr=2πnR可得:转速的最小值n=240 r/min(或4 r/s).
(3)传送带的速度越大,“痕迹”越长.当面粉的痕迹布满整条传送带时,痕迹达到最长.即痕迹长Δs=2l+2πR=18.0 m
在面粉袋由A端运动到B端的时间内,传送带运转的距离s带=Δs+lAB=26.0 m
又由(2)已知t′=2.0 s
故而有:2πn′R≥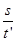
则:n′≥390 r/min(或6.5 r/s).
把面粉放传送带上,受摩擦力提供加速度,由匀变速直线运动公式可求得面粉与传送带速度相同时所用时间和位移,当面粉速度与传送带速度相同之后随传送带一起匀速运动,要想运动时间最短,面粉应一直做匀加速直线运动,由此可求得末端速度大小,即为传送带速度大小

 阅读快车系列答案
阅读快车系列答案
 m的主动轮Q1和从动轮Q2及传送带等构成.两轮轴心相距lAB=8.0 m,轮与传送带不打滑.现用此装置运送一袋面粉,已知这袋面粉与传送带之间的动摩擦因数μ=0.4,这袋面粉中的面粉可不断地从袋中渗出.(g取10 m/s2)
m的主动轮Q1和从动轮Q2及传送带等构成.两轮轴心相距lAB=8.0 m,轮与传送带不打滑.现用此装置运送一袋面粉,已知这袋面粉与传送带之间的动摩擦因数μ=0.4,这袋面粉中的面粉可不断地从袋中渗出.(g取10 m/s2)
