题目内容
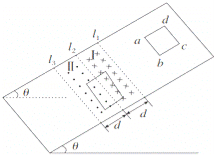
【题目】如图所示,两根平行的光滑金属导轨MN、PQ放在水平面上,左端向上弯曲,导轨间距为L,电阻不计,水平段导轨所处空间存在方向竖直向上的匀强磁场,磁感应强度为B.导体棒a与b的质量均为m,电阻值分别为Ra=R,Rb=2R.b棒放置在水平导轨上足够远处,a棒在弧形导轨上距水平面h高度处由静止释放.运动过程中导体棒与导轨接触良好且始终与导轨垂直,重力加速度为g.
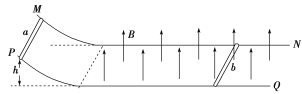
(1)求a棒刚进入磁场时受到的安培力的大小和方向;
(2)求最终稳定时两棒的速度大小;
(3)从a棒开始下落到最终稳定的过程中,求b棒上产生的内能.
【答案】(1) ![]() ,方向水平向左 (2)
,方向水平向左 (2) ![]()
![]() (3)
(3)![]() mgh
mgh
【解析】(1)设a棒刚进入磁场时的速度为v,从开始下落到进入磁场
根据机械能守恒定律有mgh=![]() mv2
mv2
a棒切割磁感线产生感应电动势E=BLv
根据闭合电路欧姆定律有I=![]()
a棒受到的安培力F=BIL
联立以上各式解得F=![]() ,方向水平向左.
,方向水平向左.
(2)设两棒最后稳定时的速度为v′,从a棒开始下落到两棒速度达到稳定
根据动量守恒定律有mv=2mv′
解得v′=![]()
![]() .
.
(3)设a棒产生的内能为Ea,b棒产生的内能为Eb
根据能量守恒定律得![]() mv2=
mv2=![]() ×2mv′2+Ea+Eb
×2mv′2+Ea+Eb
两棒串联内能与电阻成正比Eb=2Ea
解得Eb=![]() mgh.
mgh.

练习册系列答案
相关题目