题目内容

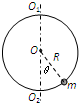放置在竖直面内的光滑铁环半径为R=0.20m，环上有一个质量为m的穿孔小球，能沿环无摩擦滑动．如果铁环绕通过其圆心的竖直轴O1O2以角速度ω=10rad/s匀速旋转，则小球相对于铁环静止时，球与圆心的连线与竖直方向的夹角是（g取10m/s2 ）（　　）
分析：小球随圆环一起绕竖直轴转动，根据几个关系求出转动半径，再根据合外力提供向心力列方程求解．
解答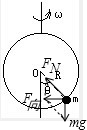：解：对小球进行受力分析，如图所示：
由几何关系得小球转动半径为：r=Rsinθ．
根据向心力公式得：mω2r=mgtanθ
联立代入数据解得：cosθ=
1
2
，则θ=60°．故C正确，A、B、D错误．
故选C．
点评：该题主要考查了向心力公式的直接应用，要求同学们能结合几何关系解题，注意小球转动半径不是R．
练习册系列答案
相关题目
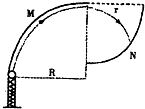如图是为了检验某种防护罩承受冲击力的装置，M是半径为R=1.0m的固定于竖直平面内的
1
4
光滑圆弧轨道，轨道上端切线水平．N为待检验的固定曲面，该曲面在竖直面内的截面为半径r=
0.69
m的
1
4
圆弧，圆弧下端切线水平且圆心恰好位于M轨道的上端点．M的下端相切处放置竖直向上的弹簧枪，可发射速度不同的质量m=0.01kg的小钢珠，假设某次发射的钢珠沿轨道恰好能经过M的上端点，水平飞出后落到曲面N的某一点上，取g=10m/s2．求：
（1）发射该钢球前，弹簧的弹性势能EP多大？
（2）钢珠从M圆弧轨道最高点飞出至落到圆弧N上所用的时间是多少（结果保留两位有效数字）？
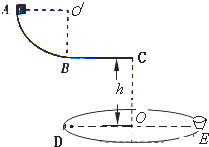（2013?德州一模）如图所示，一半径R=1m的圆盘水平放置，在其边缘 E点固定一小桶（可视为质点）．在圆盘直径 DE 的正上方平行放置一水平滑道 BC，滑道右端 C点 与圆盘圆心O在同一竖直线上，且竖直高度 h=1.25m．AB为一竖直面内的光滑四分之一圆弧轨道，半径r=0.45m，且与水平滑道相切与B点．一质量m=0.2kg的滑块（可视为质点）从A点由静止释放，当滑块经过B点时，圆盘从图示位置以一定的角速度ω绕通过圆心的竖直轴匀速转动，最终物块由C 点水平抛出，恰好落入圆盘边缘的小桶内．已知滑块与滑道 BC间的摩擦因数μ=0.2．（取g=10m/s2）求
（1）滑块到达B点时对轨道的压力
（2）水平滑道 BC的长度；
（3）圆盘转动的角速度ω应满足的条件．
如图所示为过山车简易模型，它是由光滑水平轨道和竖直面内的光滑圆轨道组成，Q点 为圆形轨道最低点，M点为最高点，圆形轨道半径R=0.32m．水平轨道PN右侧的水平 地面上，并排放置两块长木板c、d，两木板间相互接触但不粘连，长木板上表面与水平轨 道PN平齐，木板c质量m3=2.2kg，长L=4m，木板d质量m4=4.4kg．质量m2=3.3kg 的小滑块b放置在轨道QN上，另一质量m1=1.3kg的小滑块a从P点以水平速度v0向 右运动，沿圆形轨道运动一周后进入水平轨道与小滑块b发生碰撞，碰撞时间极短且碰 撞过程中无机械能损失．碰后a沿原路返回到M点时，对轨道压力恰好为0．已知小滑 块b与两块长木板间动摩擦因数均为μ0=0.16，重力加速度g=10m/s2．
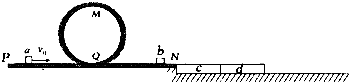精英家教网（1）求小滑块a与小滑块b碰撞后，a和b的速度大小v1和v2；
（2）若碰后滑块b在木板c、d上滑动时，木板c、d均静止不动，c、d与地面间的动摩擦因 数μ至少多大？（木板c、d与地面间的动摩擦因数相同，最大静摩擦力等于滑动摩擦 力）
（3）若不计木板c，d与地面间的摩擦，碰后滑块b最终恰好没有离开木板d，求滑块b在 木板c上滑行的时间及木板d的长度．
精英家教网如图所示装置是检验某种防护罩承受冲击力的装置示意图，M是半径为R=1.0m的固定于竖直平面内的
1
4
光滑圆弧轨道，轨道上端的切线沿水平方向．N为待检验的固定曲面防护罩，该曲面在竖直面内的截面为半径r=
0.69
m的
1
4
圆弧，圆弧下端切线水平且圆心恰好位于M轨道的上端点．M下端的相切处放置一竖直向上的弹簧枪，可发射速度不同的质量m=0.01kg的同样规格的小钢珠，取g=10m/s2．求：
（1）假设某次发射的钢珠沿轨道恰好能经过M的上端点，试求钢球发射前，弹簧的弹性势能EP应多大？
（2）在满足（1）的情况下，试估算钢球从离开弹簧至打到N板所用的时间？并讨论随发射初的弹性势能的进一步增大，钢球从离开弹簧至打到N板所用的时间将发生怎样的变化（需说明理由）？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网