题目内容
10. 如图所示,小球甲从空中A点以vA=3m/s的速度竖直向下抛出,同时另一个小球乙从A点正下方H=10m的B点以vB=4m/s的速度水平抛出.不计空气阻力,B点离地面足够高.求:
如图所示,小球甲从空中A点以vA=3m/s的速度竖直向下抛出,同时另一个小球乙从A点正下方H=10m的B点以vB=4m/s的速度水平抛出.不计空气阻力,B点离地面足够高.求:(1)经过多长时间两球在空中的距离最短?
(2)最短距离是多少?
分析 A做竖直下抛运动,B做平抛运动,设经过时间t位移最短,根据运动学基本规律求出两球之间的距离的表达式,结合数学知识即可求解.
解答 解:经过时间t,A做竖直下抛运动的位移为:${y}_{甲}={v}_{A}t+\frac{1}{2}g{t}^{2}$
B在竖直方向做自由落体运动的位移为:${y}_{乙}=\frac{1}{2}g{t}^{2}$
两球在竖直方向的距离为:y=H+y乙-y甲
B在水平方向的位移,即两球在水平方向的距离为:x=υBt
所以,两球之间的距离为:$s=\sqrt{{x}^{2}+{y}^{2}}$,
联立以上各式解得:s=$\sqrt{(10-3t)^{2}+(4t)^{2}}$
当t=1.2s时,两球之间最短距离为smin=8m.
答:(1)经过1.2s时间两球在空中的距离最短.
(2)最短距离是8m.
点评 本题主要考查了竖直下抛运动和做平抛运动的基本规律,求某个量的极值时可以先把这个量的表达式求出来,再结合数学知识求解,难度适中.

练习册系列答案
相关题目
20.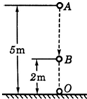 如图所示,小球从距地面5m高处落下,被地面反向弹回后,在距地面2m高处被接住,则小球从高处落下到被接住这一过程中通过的路程和位移的大小分别是( )
如图所示,小球从距地面5m高处落下,被地面反向弹回后,在距地面2m高处被接住,则小球从高处落下到被接住这一过程中通过的路程和位移的大小分别是( )
 如图所示,小球从距地面5m高处落下,被地面反向弹回后,在距地面2m高处被接住,则小球从高处落下到被接住这一过程中通过的路程和位移的大小分别是( )
如图所示,小球从距地面5m高处落下,被地面反向弹回后,在距地面2m高处被接住,则小球从高处落下到被接住这一过程中通过的路程和位移的大小分别是( )| A. | 7 m 7 m | B. | 5 m 2 m | C. | 5 m 3 m | D. | 7 m 3 m |
1.如图所示的电路中,灯泡A1、A2的规格完全相同,自感线圈L的电阻可以忽略,下列说法中正确的是( )
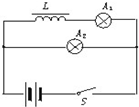

| A. | 当接通电路时,A1和A2始终一样亮 | |
| B. | 当接通电路时,A2先亮,A1后亮,最后A2和A1一样亮 | |
| C. | 当断开电路时,A1和A2都过一会儿熄灭 | |
| D. | 当断开电路时,A2立即熄灭,A1过一会儿熄灭 |
18.当质量一定的物体动能不变时,下列说法正确的是( )
| A. | 物体一定做匀速直线运动 | B. | 物体所受合外力一定为零 | ||
| C. | 物体可能做曲线运动 | D. | 物体的速度大小一定不变 |
12.物体做匀加速直线运动,加速度a=2m/s2,那么( )
| A. | 物体任意1秒的末速度一定等于初速度的2倍 | |
| B. | 物体任意1秒的末速度一定比初速度大2m/s | |
| C. | 物体这1秒的初速度一定比前1秒的末速度大2m/s | |
| D. | 物体在每1秒内速度大小增加2m/s |
