题目内容
 在同一介质中两列横波沿x轴相向传播,波源分别位于x1=0和x2=1.4m处,波速均为0.4m/s,振幅均为2cm.如图所示为t=0时刻两列波的图象,此刻P、Q两质点恰好开始振动.下列说法中正确的是( )
在同一介质中两列横波沿x轴相向传播,波源分别位于x1=0和x2=1.4m处,波速均为0.4m/s,振幅均为2cm.如图所示为t=0时刻两列波的图象,此刻P、Q两质点恰好开始振动.下列说法中正确的是( )分析:根据波位移公式△x=v?△t计算波的位移,得到任意时刻波形图,得到各个质点的合位移,分析M点的位移情况.
解答:解:A、两列波均在传播,故相遇时间:△t=
=
s=0.75s,故A正确;
B、由图可知,λ=0.4m,所以T=
=
s=1s,在t=1.5s 时,P质点完成1
T,则仍在平衡位置,故B正确;
C、两列波单独传播引起的M点的位移总是相反,故振动减弱,振幅为0,故C错误;
D、由图可知,λ=0.4m,所以T=
=
s=1s,在t=1.25s 时,左边波传到N点0.5s,再经过0.75s,使得处于波峰位置,而右边波传播到N点,时间为1s,
再经过0.25s,处于波峰,因此N点在平衡位置上方,故D错误;
故选AB.
| △x |
| 2v |
| 1-0.4 |
| 2×0.4 |
B、由图可知,λ=0.4m,所以T=
| λ |
| v |
| 0.4 |
| 0.4 |
| 1 |
| 2 |
C、两列波单独传播引起的M点的位移总是相反,故振动减弱,振幅为0,故C错误;
D、由图可知,λ=0.4m,所以T=
| λ |
| v |
| 0.4 |
| 0.4 |
再经过0.25s,处于波峰,因此N点在平衡位置上方,故D错误;
故选AB.
点评:本题关键是明确波位移△x=v?△t,然后通过画波形图得到各个指点的位移,合成得到合位移.

练习册系列答案
相关题目
 在同一介质中两列横波沿x轴相向传播,波源分别位于x1=0和x2=1.4m处,波速均为0.4m/s,振幅均为2cm.如图所示为t=0时刻两列波的图象,此刻P、Q两质点恰好开始振动.下列说法中正确的是( )
在同一介质中两列横波沿x轴相向传播,波源分别位于x1=0和x2=1.4m处,波速均为0.4m/s,振幅均为2cm.如图所示为t=0时刻两列波的图象,此刻P、Q两质点恰好开始振动.下列说法中正确的是( )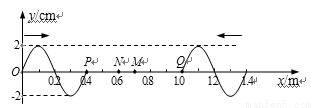
 在同一介质中两列横波沿x轴相向传播,波源分别位于x1=0和x2=1.4m处,波速均为0.4m/s,振幅均为2cm.如图所示为t=0时刻两列波的图象,此刻P、Q两质点恰好开始振动.下列说法中正确的是( )
在同一介质中两列横波沿x轴相向传播,波源分别位于x1=0和x2=1.4m处,波速均为0.4m/s,振幅均为2cm.如图所示为t=0时刻两列波的图象,此刻P、Q两质点恰好开始振动.下列说法中正确的是( )