题目内容
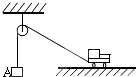 如图所示,在不计滑轮摩擦和绳子质量的条件下,当小车匀速向右运动时,物体A的运动及受力情况是( )
如图所示,在不计滑轮摩擦和绳子质量的条件下,当小车匀速向右运动时,物体A的运动及受力情况是( )分析:将小车的速度分解为沿绳子方向和垂直于绳子方向,沿绳子方向的速度等于A的速度,根据平行四边形定则判断出A的速度变化,从而得出A的加速度方向,根据牛顿第二定律判断拉力和重力的大小关系.
解答:解: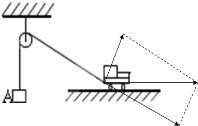 小车沿绳子方向的速度等于A的速度,设绳子与水平方向的夹角为θ,根据平行四边形定则,物体A的速度vA=vcosθ,小车匀速向右运动时,θ减小,则A的速度增大,所以A加速上升,加速度方向向上,根据牛顿第二定律有:T-GA=mAa.知拉力大于重力.故A、C正确,B、D错误.
小车沿绳子方向的速度等于A的速度,设绳子与水平方向的夹角为θ,根据平行四边形定则,物体A的速度vA=vcosθ,小车匀速向右运动时,θ减小,则A的速度增大,所以A加速上升,加速度方向向上,根据牛顿第二定律有:T-GA=mAa.知拉力大于重力.故A、C正确,B、D错误.
故选AC.
 小车沿绳子方向的速度等于A的速度,设绳子与水平方向的夹角为θ,根据平行四边形定则,物体A的速度vA=vcosθ,小车匀速向右运动时,θ减小,则A的速度增大,所以A加速上升,加速度方向向上,根据牛顿第二定律有:T-GA=mAa.知拉力大于重力.故A、C正确,B、D错误.
小车沿绳子方向的速度等于A的速度,设绳子与水平方向的夹角为θ,根据平行四边形定则,物体A的速度vA=vcosθ,小车匀速向右运动时,θ减小,则A的速度增大,所以A加速上升,加速度方向向上,根据牛顿第二定律有:T-GA=mAa.知拉力大于重力.故A、C正确,B、D错误.故选AC.
点评:解决本题的关键知道小车沿绳子方向的分速度等于物体A的速度,根据平行四边形定则进行分析.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
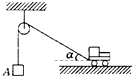 如图所示,在不计滑轮摩擦和绳子质量的条件下,当小车匀速向右运动时,物体A的运动及受力情况是( )
如图所示,在不计滑轮摩擦和绳子质量的条件下,当小车匀速向右运动时,物体A的运动及受力情况是( )| A、加速上升 | B、减速上升 | C、拉力等于重力 | D、拉力小于重力 |
 (2011?无为县模拟)如图所示,在不计滑轮摩擦和绳子质量的条件下,当小车匀速向右运动时,物体A的受力情况是( )
(2011?无为县模拟)如图所示,在不计滑轮摩擦和绳子质量的条件下,当小车匀速向右运动时,物体A的受力情况是( ) 如图所示,在不计滑轮摩擦和绳子质量的条件下,当小车匀速向右运动时,物体A的运动及受力情况是( )
如图所示,在不计滑轮摩擦和绳子质量的条件下,当小车匀速向右运动时,物体A的运动及受力情况是( ) 如图所示,在不计滑轮摩擦和绳子质量的条件下,当小车匀速向左运动时,物体A的受力情况是( )
如图所示,在不计滑轮摩擦和绳子质量的条件下,当小车匀速向左运动时,物体A的受力情况是( )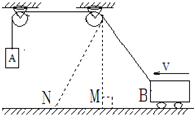 如图所示,在不计滑轮摩擦和绳子质量的条件下,小车匀速地从B点运动到M点,再 运动到N点的过程中,关于物体A的运动和受力情况,下列说法正确的是( )
如图所示,在不计滑轮摩擦和绳子质量的条件下,小车匀速地从B点运动到M点,再 运动到N点的过程中,关于物体A的运动和受力情况,下列说法正确的是( )