题目内容
5.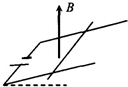 如图所示,两根平行放置的金属导轨框架与水平面的夹角为θ,导轨间距离为L,有一根垂直于导轨放置的质量为m的均匀金属棒.电源的电动势为E,内电阻为r,导轨和金属棒的总电阻为R,整个装置位于竖直向上的匀强磁场中.
如图所示,两根平行放置的金属导轨框架与水平面的夹角为θ,导轨间距离为L,有一根垂直于导轨放置的质量为m的均匀金属棒.电源的电动势为E,内电阻为r,导轨和金属棒的总电阻为R,整个装置位于竖直向上的匀强磁场中.(1)要使金属棒静止,磁感应强度B为多大?
(2)若磁场方向课改变,要使金属棒静止,磁感应强度B至少为多少?方向如何?
分析 (1)由闭合电路的欧姆定律求的电流,对导体棒受力分析根据共点力平衡求的磁场强度;
(2)对导体棒受力分析,根据三角形定则判断出安培力的最小值,根据左手定则判断出磁场方向
解答 解:(1)回路中的电流为I=$\frac{E}{R+r}$
对导体棒受力分析,根据共点力平衡可得mgsinθ=BILcosθ
解得B=$\frac{mg(R+r)tanθ}{EL}$
(2)当磁场方向沿斜面向上时,此时的磁场强度最小,故
mgsinθ=BIL
解得B=$\frac{mg(R+r)sinθ}{EL}$
答:(1)要使金属棒静止,磁感应强度B为$\frac{mg(R+r)tanθ}{EL}$
(2)若磁场方向课改变,要使金属棒静止,磁感应强度B至少为$\frac{mg(R+r)sinθ}{EL}$,方向沿斜面向上
点评 本题借助安培力考查了平衡条件的应用,判断安培力的方向时要注意安培力一定与B垂直、与I垂直

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
15.物理学的发展极大地丰富了人类对物质世界的认识,推动了科学技术的创新和革命,促进了人类文明的进步,下列说法正确的是( )
| A. | 亚里士多德首先提出了惯性的概念 | |
| B. | 伽利略对自由落体运动研究方法的核心是:把实验和逻辑推理(包括数学演算)结合起来,从而发展了人类的科学思维方式和科学研究方法 | |
| C. | 牛顿第一定律、牛顿第二定律都能通过现代的实验手段直接验证 | |
| D. | 摩托车转弯时,车手一方面要适当的控制速度,另一方面要将身体稍微向里倾斜,这是为了通过减少人和车的惯性达到安全行驶的目的 |
20.某物体以30m/s的初速度竖直上抛,不计空气阻力,g取10m/s2.4s内物体的( )
| A. | 路程为50m | B. | 位移大小为40m,方向向上 | ||
| C. | 速度改变量的大小为20m/s | D. | 平均速度大小为10m/s,方向向上 |
17.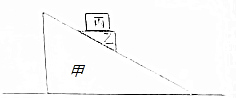 如图所示,质量为M的斜面甲放在粗糙的水平面上,当质量为m的物体乙沿斜面匀速下滑时,斜面静止不动,如果在乙物体上叠放物体丙,会出现乙和丙一起沿叙面下滑的现象.对此,以下说法正确的是( )
如图所示,质量为M的斜面甲放在粗糙的水平面上,当质量为m的物体乙沿斜面匀速下滑时,斜面静止不动,如果在乙物体上叠放物体丙,会出现乙和丙一起沿叙面下滑的现象.对此,以下说法正确的是( )
 如图所示,质量为M的斜面甲放在粗糙的水平面上,当质量为m的物体乙沿斜面匀速下滑时,斜面静止不动,如果在乙物体上叠放物体丙,会出现乙和丙一起沿叙面下滑的现象.对此,以下说法正确的是( )
如图所示,质量为M的斜面甲放在粗糙的水平面上,当质量为m的物体乙沿斜面匀速下滑时,斜面静止不动,如果在乙物体上叠放物体丙,会出现乙和丙一起沿叙面下滑的现象.对此,以下说法正确的是( )| A. | 乙和丙将加速下滑 | |
| B. | 乙和丙仍匀速下滑 | |
| C. | 斜面对乙的作用力竖直向上,大小仍为mg | |
| D. | 若斜面不动,将会受到水平向右的摩擦力 |
14.如图,球A,B质量都是m,把与A相连的上端绳剪断,关于球A球和B的加速度aA、aB,下列说法正确的是( )


| A. | 绳断瞬间,aA=aB=0 | B. | 绳断瞬间aA=2g,aB=0 | ||
| C. | 当弹簧回复原长时,aA=aB=g | D. | 在弹簧第一次恢复原长前aA>aB |
11.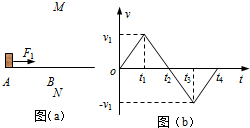 静止在光滑水平面上质量为m的小物块,在直线MN的左边只受到水平力F1作用(小物块可视为质点),在MN的右边除受F1外还受到与F1在同一条直线上的恒力F2作用,现使小物块由A点从静止开始运动,如图(a)所示,小物块运动的v-t图象如图(b)所示,下列说法中正确的是( )
静止在光滑水平面上质量为m的小物块,在直线MN的左边只受到水平力F1作用(小物块可视为质点),在MN的右边除受F1外还受到与F1在同一条直线上的恒力F2作用,现使小物块由A点从静止开始运动,如图(a)所示,小物块运动的v-t图象如图(b)所示,下列说法中正确的是( )
 静止在光滑水平面上质量为m的小物块,在直线MN的左边只受到水平力F1作用(小物块可视为质点),在MN的右边除受F1外还受到与F1在同一条直线上的恒力F2作用,现使小物块由A点从静止开始运动,如图(a)所示,小物块运动的v-t图象如图(b)所示,下列说法中正确的是( )
静止在光滑水平面上质量为m的小物块,在直线MN的左边只受到水平力F1作用(小物块可视为质点),在MN的右边除受F1外还受到与F1在同一条直线上的恒力F2作用,现使小物块由A点从静止开始运动,如图(a)所示,小物块运动的v-t图象如图(b)所示,下列说法中正确的是( )| A. | 在B点的右边加速度大小为$\frac{{v}_{1}}{{t}_{2}-{t}_{1}}$ | |
| B. | 小物块在经过B点后向右运动的时间为t2-t1 | |
| C. | F2的大小为$\frac{m{v}_{1}}{{t}_{2}-{t}_{1}}$ | |
| D. | 小物块在B点右边运动的最大距离为$\frac{{v}_{1}({t}_{2}-{t}_{1})}{2}$ |
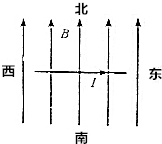 在赤道上,地磁场可以看成沿南北方向并且与地面平行的匀强磁场.如果在赤道上有一条沿东西方向的水平直导线,长为20m,导线中通有由西向东的电流30A.地磁场对这根导线的作用力大小为0.03N.试求:
在赤道上,地磁场可以看成沿南北方向并且与地面平行的匀强磁场.如果在赤道上有一条沿东西方向的水平直导线,长为20m,导线中通有由西向东的电流30A.地磁场对这根导线的作用力大小为0.03N.试求: