题目内容
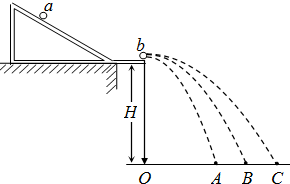
某同学用如图所示的装置通过半径相同的A、B两球的碰撞来验证碰撞中的动量守恒,实验时先使A球从斜槽上某一固定位置G由静止开始滚下,落到位于水平地面的记录纸上,留下痕迹,重复上述操作10次,得到10个落点痕迹,再把B球放在水平槽上靠近槽末端的支柱上,让A球仍从位置G由静止开始滚下,和B球碰撞后,A、B球分别在记录纸上留下各自的落点痕迹,重复这种操作10次,图中O点是水平槽末端在记录纸上的垂直投影点,B球落点痕迹如图,其中米尺水平放置,米尺的零点与O点对齐
(1)从图中可以测出碰撞后B球的水平射程应取为______cm.
(2)若A球和B球的质量分别为mA和mB,球的直径为d,OM的距离为S1,OP的距离为S2,ON的距离为S3,则验证碰撞中的动量守恒的表达式为______.

(1)从图中可以测出碰撞后B球的水平射程应取为______cm.
(2)若A球和B球的质量分别为mA和mB,球的直径为d,OM的距离为S1,OP的距离为S2,ON的距离为S3,则验证碰撞中的动量守恒的表达式为______.

(1)由图示可知,刻度尺分度值为1mm,B球碰后的落点是N,
由图示可知,ON=80.42cm,碰撞后B球的水平射程为ON-d=80.42cm-0.15cm=80.27;
(2)两球离开轨道后做平抛运动,它们抛出点的高度相等,它们在空中的运动时间t相等,
如果动量守恒,则满足:mAvA=mAvA′+mBvB,两边同时乘以运动时间t,
得:mAvAt=mAvA′t+mBvBt,即:mAOP=mAOM+mB(0N-d),mAs2=mAs1+mB(s3-d);
故答案为:(1)80.27;(2)mAs2=mAs1+mB(s3-d).
由图示可知,ON=80.42cm,碰撞后B球的水平射程为ON-d=80.42cm-0.15cm=80.27;
(2)两球离开轨道后做平抛运动,它们抛出点的高度相等,它们在空中的运动时间t相等,
如果动量守恒,则满足:mAvA=mAvA′+mBvB,两边同时乘以运动时间t,
得:mAvAt=mAvA′t+mBvBt,即:mAOP=mAOM+mB(0N-d),mAs2=mAs1+mB(s3-d);
故答案为:(1)80.27;(2)mAs2=mAs1+mB(s3-d).

练习册系列答案
相关题目